上海市普陀区2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-02 类型:期中考试
一、单选题
-
1. 下列函数中,是二次函数的为( )A、 B、 C、 D、2. 下列命题中,正确的是( )A、所有的矩形都相似; B、所有的等腰梯形都相似; C、所有的等边三角形都相似; D、含有 角的所有等腰三角形都相似3. 如图,已知 , ,那么下列结论中,正确的是( )
 A、 B、 C、 D、4. 已知二次函数 的图像如图所示,那么 、 、 的符号为( )
A、 B、 C、 D、4. 已知二次函数 的图像如图所示,那么 、 、 的符号为( ) A、 B、 C、 D、5. 已知 、 、 都是非零向量,下列条件中,不能判断 的是( )A、 B、 C、 , D、6. 如图,四边形 的对角线 与 相交于点 , , , , ,那么下列结论中,错误的是( )
A、 B、 C、 D、5. 已知 、 、 都是非零向量,下列条件中,不能判断 的是( )A、 B、 C、 , D、6. 如图,四边形 的对角线 与 相交于点 , , , , ,那么下列结论中,错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 如果 ,那么 .8. 已知点 在线段 上,且 ,那么 的值是.9. 如果二次函数 的图像经过原点,那么 的值是.10. 将抛物线 向右平移5个单位,那么平移后所得的新抛物线的表达式是.11. 二次函数 的图像与 轴的交点坐标是.12. 如果点 、 是二次函数 的图像上两点,那么 .(填“>”、“=”或“<”)13. 一个边长为3厘米的正方形,若它的边长增加x厘米,面积随之增加y平方厘米,则y关于x的函数表达式是 .14. 如图,平行四边形 中,点 在边 上, 交 于点 ,如果 ,那么 的值是.
 15. 如图,已知△ 中, , ,点 、 分别在边 、 上, , ,那么 的长是.
15. 如图,已知△ 中, , ,点 、 分别在边 、 上, , ,那么 的长是.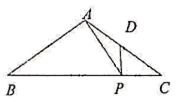 16. 如图,在 中, , 于点 ,如果 ,那么 的值是.
16. 如图,在 中, , 于点 ,如果 ,那么 的值是.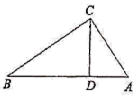 17. 已知 是△ 的重心,设 , ,那么 =(用 、 表示).
17. 已知 是△ 的重心,设 , ,那么 =(用 、 表示).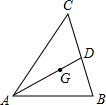 18. 如图, 中, , ,将 绕点 顺时针旋转得到 ,点 的对应点 落在边 上,已知 , ,则 的长为.
18. 如图, 中, , ,将 绕点 顺时针旋转得到 ,点 的对应点 落在边 上,已知 , ,则 的长为.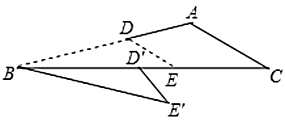
三、解答题
-
19. 如图,已知两个不平行的向量 、 .先化简,再求作: .(不要求写作法,但要保留作图痕迹,并指出所作图中表示结论的向量)
 20. 已知二次函数的图象经过 、 、 三点.(1)、求这个二次函数的解析式;(2)、求出图像的顶点坐标.21. 在平面直角坐标系 中,抛物线 与 轴的负半轴交于点 、与 轴交于点 ,且 .(1)、求 的值;(2)、如果点 是抛物线上一点,联结 交 轴正半轴于点 , ,求 的坐标.22. 已知:如图, .
20. 已知二次函数的图象经过 、 、 三点.(1)、求这个二次函数的解析式;(2)、求出图像的顶点坐标.21. 在平面直角坐标系 中,抛物线 与 轴的负半轴交于点 、与 轴交于点 ,且 .(1)、求 的值;(2)、如果点 是抛物线上一点,联结 交 轴正半轴于点 , ,求 的坐标.22. 已知:如图, . (1)、求证:△ ∽△ ;(2)、如果 , , , ,求 的长.23. 已知:如图,在△ 中, , 是边 上的中线, 于点 , 与 交于点 .
(1)、求证:△ ∽△ ;(2)、如果 , , , ,求 的长.23. 已知:如图,在△ 中, , 是边 上的中线, 于点 , 与 交于点 . (1)、求证: ;(2)、过点 作 交 的延长线于点 .求证:
(1)、求证: ;(2)、过点 作 交 的延长线于点 .求证: