上海市浦东新区南片联合体2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列根式中与 $\sqrt{\frac{b}{a}}$ 不是同类二次根式的是（）

A、 $\sqrt{a b}$ B、 $\sqrt{\frac{a}{b}}$ C、 $3 \sqrt{a b}$ D、 $\sqrt{a b^{2}}$

查看试题解析
2. 下列化简错误的是（）

A、 $\sqrt{\frac{16}{25}} = \frac{4}{5}$ B、 $\sqrt{1 \frac{9}{16}} = 1 \frac{3}{4}$ C、 $\sqrt{\frac{27}{64}} = \frac{3}{8} \sqrt{3}$ D、 $- \sqrt{7 \frac{1}{5}} = - \frac{6}{5} \sqrt{5}$

查看试题解析
3. 关于x的方程 $(m^{2} - m) x^{2} + m x + 2 = 0$ 是一元二次方程的条件是（）

A、 $m \neq 0$ B、 $m \neq 1$ C、 $m \neq 0$ 或 $m \neq 1$ D、 $m \neq 0$ 且 $m \neq 1$

查看试题解析
4. 下列二次三项式在实数范围内不能因式分解的是（）

A、 $6 x^{2} + x - 15$ B、 $3 y^{2} + 7 y + 3$ C、 $x^{2} - 2 x - 4$ D、 $2 x^{2} - 4 x y + 5 y^{2}$

查看试题解析
5. 下列命题中是真命题的是（）

A、有两边和其中一边的对角对应相等的两个三角形全等 B、两条平行直线被第三条直线所截，则一组同旁内角的平分线互相垂直 C、三角形的一个外角等于两个内角的和 D、等边三角形既是中心对称图形，又是轴对称图形

查看试题解析
6. 如图，△ABC中，点D、E分别在AB、AC边上，AD=BD，AE=EC，BC=6，则DE=（）

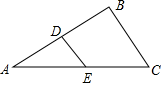A、4 B、3 C、2 D、5

查看试题解析

二、填空题

7. 当 $x$ 时， $\sqrt{— \frac{1}{x}}$ 无意义．

查看试题解析
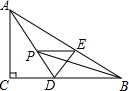
8. 写出 $\sqrt{x} + \sqrt{2 y}$ 的一个有理化因式.

查看试题解析
9. 一家今年刚成立的小型快递公司业务量逐月攀升，今年7月份和9月份完成投送的快递件数分别是20万件和24.2万件．若假设该公司每月投送的快递件数的增长率相同，则这家公司投送快递件数的月平均增长率为．

查看试题解析
10. $\sqrt{\frac{27}{16}} + \sqrt{1 \frac{1}{3}} =$ .

查看试题解析
11. $\sqrt{54 a b} \div \sqrt{\frac{9 b}{a^{2}}} (a > 0, b > 0)$ =.

查看试题解析
12. 化简 $\sqrt{- a^{3}} =$ .

查看试题解析
13. 不等式 $\sqrt{2} x - 1 < \sqrt{3} x$ 的解集是．

查看试题解析
14. 命题“等角的余角相等”的逆命题是：.

查看试题解析
15. 在△ABC中，若其中一个内角等于另外两个内角的差，则必有一个内角等于°.

查看试题解析
16. 如图，在Rt△ABC中，∠C=90°，∠ABC=30°，点D是BC边上的点，CD=1，将△ACD沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则PB+PE的最小值是．

查看试题解析
17. 如图，在平面内，两条直线L₁ ， L₂相交于点O，对于平面内任意一点M，若p，q分别是点M到直线L₁ ， L₂的距离，则称(p，q)为点M的“距离坐标”.根据上述规定，“距离坐标”是(2，1)的点共有个

查看试题解析
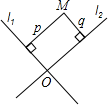18. 如图，正方形ABCD和正方形AEFG中，点E在AD上，如果AB=3，那么△BDF的面积等于．

查看试题解析

三、解答题

19. 计算:

(1)、 $4 \sqrt{\frac{9}{8}} \times \frac{1}{2} \sqrt{\frac{9}{50}} - \sqrt{\frac{9}{28}} \div \sqrt{1 \frac{1}{35}}$

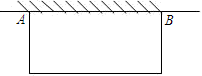
(2)、计算： $\frac{2}{y} \sqrt{x y^{3}} - \sqrt{x^{3} y} - \frac{1}{x} \sqrt{x^{3} y}$ （ $x$ >0， $y$ >0）

查看试题解析
20. 解方程：

(1)、（x-1）（x+3）=5

(2)、x²+x-3=0（公式法）

查看试题解析
21. 在实数范围内将下列二次三项式分解因式：

(1)、x²-7x-78；

(2)、4x²+4x-3；

查看试题解析
22. 已知关于的x方程 $4 x^{2} - (k + 2) x + k = 1$ 有两个相等的实数根，求k的值及这时方程的根.

查看试题解析
23. 如图，某农户发展养禽业，准备利用现有的34米长的篱笆靠墙AB（墙长为25米）围成一个面积为120平方米的长方形养鸡场，这个养鸡场的长和宽各是多少？

查看试题解析
24. 已知：如图所示，AD是△ABC的角平分线，AD的垂直平分线交AB于点F，交BC的延长线于点E，交AC于点G．求证：∠CAE=∠B．

查看试题解析
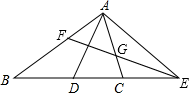25. 如图：在△ABC中，∠ACB=90°，AC=BC，过点C在△ABC外作直线MN，AM⊥MN于M，BN⊥MN于N．

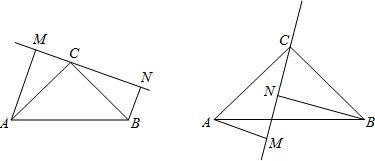(1)、求证：MN=AM+BN．

(2)、若过点C在△ABC内作直线MN，AM⊥MN于M，BN⊥MN于N，则AM、BN与MN之间有什么关系？请说明理由．

查看试题解析
26. 点O在△ABC的内部，点D，E，F，G分别是AB，OB，OC，AC的中点．

(1)、如图1，求证：四边形DEFG是平行四边形；

(2)、如图2，射线AO交BC边于点H，连接DH，GH，若AB=AC，DE⊥EF，在不添加任何辅助线的情况下，请直接写出图2中所有的等腰三角形（不包含以∠BAC为内角的三角形）．

查看试题解析