黑龙江省佳木斯市桦南县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-02 类型：期中考试
一、单选题
-
1. 下面有4个汽车商标图案，其中是轴对称图形的是（ ）
A、 B、 C、 D、2. 以下列各组线段为边，能组成三角形的是（ ）A、2cm，3cm，5cm B、5cm，6cm，10cm C、1cm，1cm，3cm D、3cm，4cm，9cm3. 一个多边形的每一个内角都等于 ，则这个多边形的内角和是（ ）A、 B、 C、 D、4. 如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（ ）
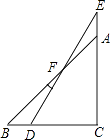A、15° B、25° C、30° D、10°5. 如图AB=CD，AD=BC，过O点的直线交AD于E，交BC于F，图中全等三角形有（ ）
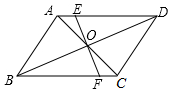A、4对 B、5对 C、6对 D、7对6. 小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第_____块去，这利用了三角形全等中的_____原理（ ）
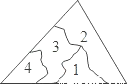A、1；SAS B、2；ASA C、3；ASA D、4；SAS7. 如图，五角星的顶点为A、B、C、D、E ， ∠A+∠B+∠C+∠D+∠E的度数为（ ）
A、90° B、180° C、270° D、360°8. 如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是（ ）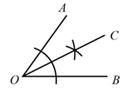
A、SAS B、ASA C、AAS D、SSS9. 如图，在△ABC中，BC边上的垂直平分线DE交边BC于点D ， 交边AB于点E ． 若△EDC的周长为24，△ABC与四边形AEDC的周长之差为12，则线段DE的长为（ ）
A、5 B、6 C、8 D、1010. 如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB ， PS⊥AC ， 垂足分别是R、S ， 若AQ=PQ ， PR=PS ， 下面四个结论：①AS=AR；②QP∥AR；③△BRP≌△QSP；④AP垂直平分RS ． 其中正确结论的序号是（ ）．
A、①② B、①②③ C、①②④ D、①②③④二、填空题
-
11. 在等腰三角形ABC中，有一边的长为4cm ， 另一边的长是8cm ， 则它的周长为cm.12. 十边形从一个顶点出发，能引出条对角线，一共有条对角线．13.
如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3= 度．
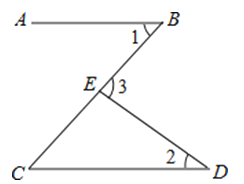14. 如图，△ABC≌△CDA ， 若AD=3cm ， AB=2cm ， 则四边形ABCD的周长= cm.
15. 如图，B、C、E共线AB⊥BE，DE⊥BE，AC⊥DC，AC=DC，又AB=2cm，DE=1cm，则BE=。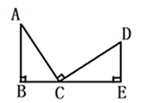
16. 在△ABC中，∠C=90°，BD平分∠ABC交AC于点D，若AC=14，且AD：DC=4：3，则点D到AB的距离是 ．17. 一个多边形截去一个角后，形成新多边形的内角和为2520°，则原多边形边数为 ．18. 如图的三角形纸片中，AB=8cm，BC=6cm，AC=5cm.沿过点B的直线折叠三角形，使点C落在AB边的点E处，折痕为BD.则△AED的周长为cm.
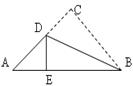19. 如图，∠DAB=∠EAC=65°，AB=AD，AC=AE，BE和CD相交于点O，AB和CD相交于P，AC和BE相交于F，则∠DOE的度数是.
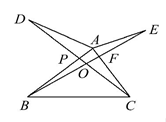20. 如图，在 ABC中， A=80 ， ABC与 ACD的平分线交于点A1 ， 得 A1； A1BC与 A1CD的平分线相交于点A2 ， 得 A2；……； A7BC与 A7CD的平分线相交于点A8 ， 得 A8 ， 则 A8的度数为.
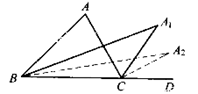.三、解答题
-
21. 已知：如图，已知△ABC中，其中A（0，﹣2），B（2，﹣4），C（4，﹣1）.
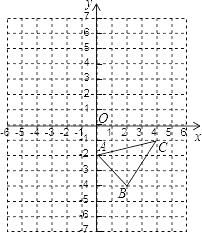(1)、画出与△ABC关于y轴对称的图形△A1B1C1；(2)、写出△A1B1C1各顶点坐标；(3)、求△ABC的面积.22. 一个多边形的内角和比它外角和的3倍少180°，求这个多边形的边数．23. 在△ABC中，AB=AC ， AC上的中线BD把三角形的周长分为24㎝和30㎝的两个部分，求三角形的三边长．24. 如图所示，已知点P是△ABC三条角平分线的交点，PD⊥AB ， 若PD=5，△ABC的周长为20，求△ABC的面积．
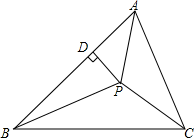25. 如图，四边形ABDC中，∠D=∠ABD=90°，点O为BD的中点，且OA⊥OC．
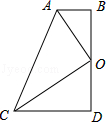(1)、求证：CO平分∠ACD；(2)、求证：AB+CD=AC．26. 如图AD是三角形ABC的中线，E ， F分别在AB ， AC上，且DF丄DE. 求证：BE+CF>EF
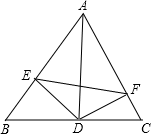27. 如图
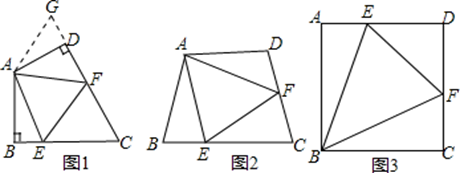(1)、如图1：在四边形ABCD中，AB=AD ， ∠BAD=120°，∠B=∠ADC=90°．E ， F分别是BC ， CD上的点．且∠EAF=60°．探究图中线段EF ， BE ， FD之间的数量关系．小明同学探究的方法是：延长FD到点G ． 使DG=BE ． 连结AG ， 先证明△ABE≌△ADG ， 再证明△AEF≌△AGF ， 可得出结论，
他的结论是（直接写结论，不需证明）；
(2)、如图2，若在四边形ABCD中，AB=AD ， ∠B+∠D=180°，E、F分别是BC ， CD上的点，且∠EAF是∠BAD的二分之一，上述结论是否仍然成立，并说明理由．(3)、如图3，四边形ABCD是边长为5的正方形，∠EBF=45°，直接写出三角形DEF的周长．