广东省广州市花都区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-02 类型:期中考试
一、单选题
-
1. 在△ABC中,∠A=40°,∠B=60°,则∠C=( )A、40° B、80° C、60° D、100°2. 下列计算中,结果是a7的是( )A、a - a B、a ·a C、a +a D、a ÷a3. 小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长为( )A、3cm B、4cm C、9cm D、10cm4. 下列图形具有稳定性的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列运算错误的是( )A、(m ) = m B、a ÷a =a C、x ·x =x D、a +a =a6. 如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( )
5. 下列运算错误的是( )A、(m ) = m B、a ÷a =a C、x ·x =x D、a +a =a6. 如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是( ) A、AD=AE B、DB=AE C、DF=EF D、DB=EC7. 如图,在△ABD与△ACD中,已知∠CAD=∠BAD,在不添加任何辅助线的前提下,依据“ASA”证明△ABD≌△ACD,需再添加一个条件,正确的是( )A、∠B=∠C B、∠BDE=∠CDE C、AB=AC D、BD=CD8. 若(x+2) (x-1)=x2+mx-2,则m的值为( )A、3 B、-3 C、1 D、-19. 如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( )
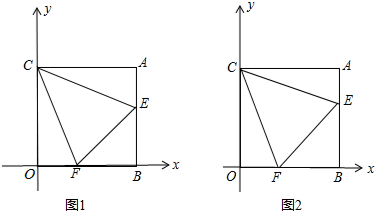
A、AD=AE B、DB=AE C、DF=EF D、DB=EC7. 如图,在△ABD与△ACD中,已知∠CAD=∠BAD,在不添加任何辅助线的前提下,依据“ASA”证明△ABD≌△ACD,需再添加一个条件,正确的是( )A、∠B=∠C B、∠BDE=∠CDE C、AB=AC D、BD=CD8. 若(x+2) (x-1)=x2+mx-2,则m的值为( )A、3 B、-3 C、1 D、-19. 如图,在CD上求一点P,使它到OA,OB的距离相等,则P点是( ) A、线段CD的中点 B、OA与OB的中垂线的交点 C、OA与CD的中垂线的交点 D、CD与∠AOB的平分线的交点10. 如图,将矩形纸片ABCD(图1)按如下步骤操作:
A、线段CD的中点 B、OA与OB的中垂线的交点 C、OA与CD的中垂线的交点 D、CD与∠AOB的平分线的交点10. 如图,将矩形纸片ABCD(图1)按如下步骤操作:( 1 )以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸片收展平,那么∠AFE的度数为( )
 A、60° B、67.5° C、72° D、75°
A、60° B、67.5° C、72° D、75°二、填空题
-
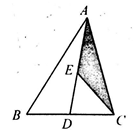
11. 计算:(5x2y) (-3x)=;12. |-2|-20190=;13. 已知:x>0,xm=6,xn=3,则xm+n的值为;14. 五边形的内角和的度数是 .15. 如图,△ABC中,点D、E分别是BC,AD的中点,且△ABC的面积为8,则阴影部分的面积是 .
 16. 在平面直角坐标系中,点A(2,0)B(0,4),作△BOC,使△BOC和△ABO全等,则点C坐标为
16. 在平面直角坐标系中,点A(2,0)B(0,4),作△BOC,使△BOC和△ABO全等,则点C坐标为三、解答题
-
17. 计算:(2m3)2+m2·m4-2m8÷m218. 计算:(24a3-6a2-3a)÷(-3a)19. 先化简,再求值:(2a+b)(a-2b)+2a(b-a),其中a=1,b=2.20. 如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠EAB=110°,∠C=60°,点D在GH上,求∠BDC的度数.
 21. 已知一个多边形的内角和是它的外角和的3倍,求这个多边形的边数.22. 如图,点D在△ABC的AB边上,且∠ACD=∠A.
21. 已知一个多边形的内角和是它的外角和的3倍,求这个多边形的边数.22. 如图,点D在△ABC的AB边上,且∠ACD=∠A. (1)、作△BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).23. 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)、作△BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法);(2)、在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明).23. 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.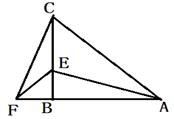 (1)、求证:Rt△ABE≌Rt△CBF(2)、若∠AEC=105°,求∠BCF的度数.
(1)、求证:Rt△ABE≌Rt△CBF(2)、若∠AEC=105°,求∠BCF的度数.