安徽省芜湖市2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-02 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若长度分别为a，3，5的三条线段能组成一个三角形，则a的值可以是（）

A、1 B、2 C、3 D、8

查看试题解析
3. 下面的多边形中，内角和与外角和相等的是（）

A、 B、 C、 D、

查看试题解析
4. 在 $△ A B C$ 中，若一个内角等于另外两个角的差，则（）

A、必有一个角等于 $30 °$ B、必有一个角等于 $45 °$ C、必有一个角等于 $60 °$ D、必有一个角等于 $90 °$

查看试题解析
5. 已知a、b、c是△ABC的三条边长，化简|a＋b－c|－|c－a－b|的结果为（）

A、2a＋2b－2c B、2a＋2b C、2c D、0

查看试题解析
6. 如图，已知 $M B = N D$ ， $∠ M B A = ∠ N D C$ ，下列不能判定 $△ A B M ≌ △ C D N$ 的条件是（）．

A、 $∠ M = ∠ N$ B、 $A B = C D$ C、 $A M = C N$ D、 $A M ∥ C N$

查看试题解析
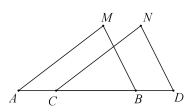7. 如图，在△ABC中，BE是∠ABC的平分线，CE是外角∠ACM的平分线，BE与CE相交于点E，若∠A=60°，则∠BEC是（）

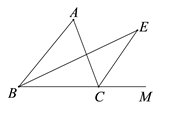A、15° B、30° C、45° D、60°

查看试题解析
8. 如图， $A B = 2$ ， $B C = A E = 6$ ， $C E = C F = 7$ ， $B F = 8$ ，则四边形ABDE与 $△ C D F$ 面积的比值是（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图所示，在 $△ A B C$ 中， $A B = A C = 5$ ，F是BC边上任意一一点，过F作 $F D ⊥ A B$ 于D ， $F E ⊥ A C$ 于E ，若 $S_{△ A B C} = 10$ ，则 $F E + F D =$ （）．

A、2 B、4 C、6 D、8

查看试题解析
10. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于D ，且 $A D = B C$ ，以AB为底边作等腰直角三角形ABE ，连接ED、EC ，延长CE交AD于点F ，下列结论：① $△ A D E ≌ △ B C E$ ；② $B D + D F = A D$ ；③ $C E ⊥ D E$ ；④ $S_{△ B D E} = S_{△ A C E}$ ，其中正确的有（）．

A、①② B、①③ C、①②③ D、①②③④

查看试题解析

二、填空题

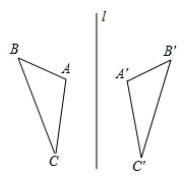
11. 如图， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 关于直线l对称，且 $∠ A = 105 °$ ， $∠ C^{'} = 30 °$ ，则 $∠ B =$ ．

查看试题解析
12. 把一副直角三角尺按如图所示的方式摆放在一起，其中 $∠ E = 90 °$ ， $∠ C = 90 °$ ， $∠ A = 45 °$ ， $∠ A = 30 °$ ，则 $∠ 1 + ∠ 2 =$ ．

查看试题解析
13. 如图，在△ABC中，DE是AC的垂直平分线，△ABC的周长为19cm ， △ABD的周长为13cm ，则AE的长为．

查看试题解析
14. 设三角形的三个内角分别为α、β、γ，且 $a \geq β \geq γ$ ， $α = 2 γ$ ，则β的最大值与最小值的和是．

查看试题解析

三、解答题

15. 尺规作图，保留作图痕迹，不写作法．

(1)、作△ABC中∠B的平分线；

(2)、作△ABC边BC上的高．

查看试题解析
16. 如图所示，在平面直角坐标系中， $△ A B C$ 的三个顶点的坐标分别为 $A (- 3 ， 2)$ ， $B (- 1 ， 3)$ ， $C (2 ， 1)$ ．

(1)、在图中作出与 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、点 $A_{1}$ 的坐标是， $S_{△ A B C} =$

查看试题解析
17. 已知：如图，C是线段AB的中点，∠A=∠B，∠ACE=∠BCD．
求证：AD=BE．

查看试题解析
18. 如果两个多边形的边数之比为1∶2，这两个多边形的内角之和为1 440°，请你确定这两个多边形的边数．

查看试题解析
19. 如图所示，六边形ABCDEF中， $C D ∥ A F$ ， $∠ C D E = ∠ B A F$ ， $A B ⊥ B C$ ， $∠ C = 120 °$ ， $∠ E = 80 °$ ，求 $∠ F$ 的度数．

查看试题解析
20. 如图，在 $△ A B C$ 中AD是BC边上的中线， $A B ∥ C E$ ，过C作AB的平行线交AD的延长线于E点．

(1)、求证： $A B = E C$ ；

(2)、若 $A B = 6$ ， $A C = 2$ ，试求中线AD的取值范围．

查看试题解析
21. 如图，树AB与树CD之间相距13m，小华从点B沿BC走向点C ，行走一段时间后他到达点E ，此时他仰望两棵大树的顶点A和D ，且两条视线的夹角正好为90°， $E A = E D$ ．已知大树AB的高为5m ，小华行走的速度为1m/s ，求小华行走到点E的时间．

查看试题解析
22. 已知BF平分 $△ A B C$ 的外角 $∠ A B E$ ，D为射线BF上一动点．

(1)、如图所示，若 $D A = D C$ ，求证： $∠ A B C = ∠ A D C$ ；

(2)、在D点运动的过程中，试比较 $B A + B C$ 与 $D C + D A$ 的大小，并说明你的理由．

查看试题解析
23. 已知：如图所示，锐角 $△ A B C$ 中，BE、CF是高，在BE的延长线上截取 $B Q = A C$ ，在CF上截取 $C P = A B$ ，再分别过点P作 $P M ⊥ B C$ 于M点，过点Q作 $Q N ⊥ B C$ 于N点

(1)、求证： $∠ Q = ∠ A C B$ ；

(2)、求证： $P M + Q N = B C$ ．

查看试题解析