2017年高考真题分类汇编（理数）：专题7 概率与统计

试卷更新日期：2017-07-21 类型：二轮复习

进入出卷网下载

一、单选题

1.
某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．
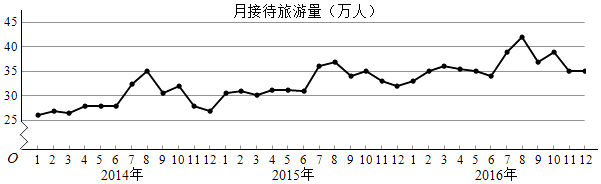
根据该折线图，下列结论错误的是（）

A、月接待游客量逐月增加 B、年接待游客量逐年增加 C、各年的月接待游客量高峰期大致在7，8月 D、各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

查看试题解析
2. 从分别标有1，2，…，9的9张卡片中不放回地随机抽取2次，每次抽取1张，则抽到在2张卡片上的数奇偶性不同的概率是（　　）

A、 $\frac{5}{18}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{7}{9}$

查看试题解析
3. 为了研究某班学生的脚长x（单位：厘米）和身高y（单位：厘米）的关系，从该班随机抽取10名学生，根据测量数据的散点图可以看出y与x之间有线性相关关系，设其回归直线方程为 $\hat{y}$ = $\hat{b}$ x+ $\hat{a}$ ，已知 $\sum_{i = 1}^{10}$ x_i=225， $\sum_{i = 1}^{10}$ y_i=1600， $\hat{b}$ =4，该班某学生的脚长为24，据此估计其身高为（　　）

A、160 B、163 C、166 D、170

查看试题解析
4. 已知随机变量ξ_i满足P（ξ_i=1）=p_i ， P（ξ_i=0）=1﹣p_i ， i=1，2．若0＜p₁＜p₂＜ $\frac{1}{2}$ ，则（）

A、E（ξ₁）＜E（ξ₂），D（ξ₁）＜D（ξ₂） B、E（ξ₁）＜E（ξ₂），D（ξ₁）＞D（ξ₂） C、E（ξ₁）＞E（ξ₂），D（ξ₁）＜D（ξ₂） D、E（ξ₁）＞E（ξ₂），D（ξ₁）＞D（ξ₂）

查看试题解析

二、填空题

5. 某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取件．

查看试题解析
6. 一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，X表示抽到的二等品件数，则DX= ．

查看试题解析
7. 记函数f（x）= $\sqrt{6 + x - x^{2}}$ 定义域为D．在区间[﹣4，5]上随机取一个数x，则x∈D的概率是．

查看试题解析

三、解答题

8. 在心理学研究中，常采用对比试验的方法评价不同心理暗示对人的影响，具体方法如下：将参加试验的志愿者随机分成两组，一组接受甲种心理暗示，另一组接受乙种心理暗示，通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用，现有6名男志愿者A₁ ， A₂ ， A₃ ， A₄ ， A₅ ， A₆和4名女志愿者B₁ ， B₂ ， B₃ ， B₄ ，从中随机抽取5人接受甲种心理暗示，另5人接受乙种心理暗示．

（Ⅰ）求接受甲种心理暗示的志愿者中包含A₁但不包含B₁的概率．
（Ⅱ）用X表示接受乙种心理暗示的女志愿者人数，求X的分布列与数学期望EX．

查看试题解析
9. 从甲地到乙地要经过3个十字路口，设各路口信号灯工作相互独立，且在各路口遇到红灯的概率分别为 $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{4}$ ．
（Ⅰ）设X表示一辆车从甲地到乙地遇到红灯的个数，求随机变量X的分布列和数学期望；
（Ⅱ）若有2辆车独立地从甲地到乙地，求这2辆车共遇到1个红灯的概率．

查看试题解析
10.
某大学艺术专业400名学生参加某次测评，根据男女学生人数比例，使用分层抽样的方法从中随机抽取了100名学生，记录他们的分数，将数据分成7组：[20，30），[30，40），…[80，90]，并整理得到如下频率分布直方图：

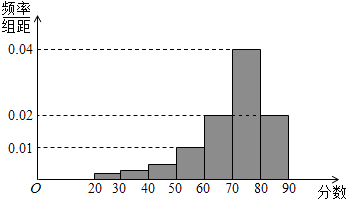
（Ⅰ）从总体的400名学生中随机抽取一人，估计其分数小于70的概率；
（Ⅱ）已知样本中分数小于40的学生有5人，试估计总体中分数在区间[40，50）内的人数；
（Ⅲ）已知样本中有一半男生的分数不小于70，且样本中分数不小于70的男女生人数相等．试估计总体中男生和女生人数的比例．

查看试题解析
11. 在平面直角坐标系xOy中，已知直线l的参数方程为 ${\begin{matrix} x = - 8 + t \\ y = \frac{t}{2} \end{matrix}$ （t为参数），曲线C的参数方程为 ${\begin{matrix} x = 2 s^{2} \\ y = 2 \sqrt{2} s \end{matrix}$ （s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．

查看试题解析
12. 为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N（μ，σ²）．

(1)、假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在（μ﹣3σ，μ+3σ）之外的零件数，求P（X≥1）及X的数学期望；

(2)、一天内抽检零件中，如果出现了尺寸在（μ﹣3σ，μ+3σ）之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
（ⅰ）试说明上述监控生产过程方法的合理性；
（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：
9.95
10.12
9.96
9.96
10.01
9.92
9.98
10.04
10.26
9.91
10.13
10.02
9.22
10.04
10.05
9.95
经计算得 $\bar{x}$ = $\frac{1}{16} \sum_{i = 1}^{16} x_{i}$ =9.97，s= $\sqrt{\frac{1}{16} \sum_{i = 1}^{16} {(x_{i} - \bar{x})}^{2}}$ = $\sqrt{\frac{1}{16} (\sum_{i = 1}^{16} x_{i}^{2} - 16 {\bar{x}}^{2})}$ ≈0.212，其中x_i为抽取的第i个零件的尺寸，i=1，2，…，16．
用样本平均数 $\bar{x}$ 作为μ的估计值 $\hat{μ}$ ，用样本标准差s作为σ的估计值 $\hat{σ}$ ，利用估计值判断是否需对当天的生产过程进行检查？剔除（ $\hat{μ}$ ﹣3 $\hat{σ} ， \hat{μ}$ +3 $\hat{σ}$ ）之外的数据，用剩下的数据估计μ和σ（精确到0.01）．
附：若随机变量Z服从正态分布N（μ，σ²），则P（μ﹣3σ＜Z＜μ+3σ）=0.9974，0.9974¹⁶≈0.9592， $\sqrt{0.008}$ ≈0.09．

查看试题解析
13.
海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100 个网箱，测量各箱水产品的产量（单位：kg），其频率分布直方图如图：
（Ⅰ）设两种养殖方法的箱产量相互独立，记A表示事件“旧养殖法的箱产量低于50kg，新养殖法的箱产量不低于50kg”，估计A的概率；
（Ⅱ）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：

箱产量＜50kg
         箱产量≥50kg
旧养殖法


新养殖法


（Ⅲ）根据箱产量的频率分布直方图，求新养殖法箱产量的中位数的估计值（精确到0.01）．
附：
P（K²≥k）
0.050
0.010
0.001
K
3.841
6.635
10.828
K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ．

查看试题解析
14. 某超市计划按月订购一种酸奶，每天进货量相同，进货成本每瓶4元，售价每瓶6元，未售出的酸奶降价处理，以每瓶2元的价格当天全部处理完．根据往年销售经验，每天需求量与当天最高气温（单位：℃）有关．如果最高气温不低于25，需求量为500瓶；如果最高气温位于区间[20，25），需求量为300瓶；如果最高气温低于20，需求量为200瓶．为了确定六月份的订购计划，统计了前三年六月份各天的最高气温数据，得下面的频数分布表：
最高气温
[10，15）
[15，20）
[20，25）
[25，30）
[30，35）
[35，40）
天数
2
16
36
25
7
4
以最高气温位于各区间的频率代替最高气温位于该区间的概率．
（Ⅰ）求六月份这种酸奶一天的需求量X（单位：瓶）的分布列；
（Ⅱ）设六月份一天销售这种酸奶的利润为Y（单位：元），当六月份这种酸奶一天的进货量n（单位：瓶）为多少时，Y的数学期望达到最大值？

查看试题解析

9.95	10.12	9.96	9.96	10.01	9.92	9.98	10.04
10.26	9.91	10.13	10.02	9.22	10.04	10.05	9.95

最高气温	[10，15）	[15，20）	[20，25）	[25，30）	[30，35）	[35，40）
天数	2	16	36	25	7	4

	箱产量＜50kg	箱产量≥50kg
旧养殖法
新养殖法

P（K²≥k）	0.050	0.010	0.001
K	3.841	6.635	10.828