广东省广州市增城区2019-2020学年七年级上学期数学期中考试试卷
试卷更新日期:2019-12-02 类型:期中考试
一、单选题
-
1. 在0,1,﹣1,2中,是负数的是( )A、0 B、1 C、﹣1 D、22. 一天早晨的气温是-3℃,中午上升到15℃,则这天中午比早晨的气温上升了( )A、15℃ B、18℃ C、-3℃ D、-18℃3. 下列选项中,与2xy是同类项的是( )A、xy B、2x2y C、-2xy2 D、x2y24. 计算(-1)×5的结果是( )A、-1 B、1 C、5 D、-55. 据广东省文化和旅游厅初步统计,2019年国庆黄金周全省共接待游客55 077 000人次,将数据55 077 000用科学记数法表示为( )A、5.5077×107 B、0.55077×107 C、5.5077×106 D、55.077×1066. 下列计算正确的是( )A、-|-2|=2 B、-12=-1 C、(-2)2=-4 D、33=97. 若长方形的周长为6m,一边长为m+n,则另一边长为( )A、3m+n B、2m+2n C、m+3 D、2m-n8. 化简整式(x-y)-(y+2x)的结果是( )A、x-2y B、–y C、-x-2y D、-x+y9. 有理数a,b如图所示,则下列结论正确的是( )
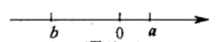 A、a>b B、|a|>|b| C、b>a D、-a< b10. 当x=1时,代数式 的值是8,则当x=-1时,这个代数式的值是( )
A、a>b B、|a|>|b| C、b>a D、-a< b10. 当x=1时,代数式 的值是8,则当x=-1时,这个代数式的值是( )
A、-8 B、-4 C、4 D、8二、填空题
-
11. 如果水位升高3m记作 ,那么水位下降6m记作12. 小薇的体重是 ,用四舍五入法将 精确到 的近似值为 .13. 多项式3x2y-2xy3-7x4y+1的次数是.14. 某水果店苹果每斤x元,提子每斤y元,昨天妈妈去该店买了2斤苹果和2斤提子;今天又去该店买了5斤苹果和3斤提子,这两天妈妈买苹果与提子一共用了元.15. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|﹣|c﹣b|的结果是 .
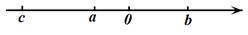 16. 在数轴上,点P表示的数是a,点P1表示的数是 ,我们称“点P1是点P的相关点”,已知数轴上A1的相关点为A2 , 点A2的相关点为A3 , 点A3的相关点为A4 , 这样依次得到点A1、A2、A3 , A4 , …,An若点A1在数轴表示的数是 ,则点A2109在数轴上表示的数是.
16. 在数轴上,点P表示的数是a,点P1表示的数是 ,我们称“点P1是点P的相关点”,已知数轴上A1的相关点为A2 , 点A2的相关点为A3 , 点A3的相关点为A4 , 这样依次得到点A1、A2、A3 , A4 , …,An若点A1在数轴表示的数是 ,则点A2109在数轴上表示的数是.三、解答题
-
17. 计算:(+12)-(-18)+(-7)-(+15)18. 计算:a+2(a-b)-3(a+b)19. 计算:-23-2×(-3)+|-5|-(-1)201920. 先化简下式,再求值:(-2x2+3+4x)-2(5x-4-x2),其中x=-2.21. 有20箱橘子,以每箱25千克为标准质量,超过的千克数用正数表示,不足的千克数用负数表示,结果记录如下
与标准质量的差值(单位:千克)
-3
-2
-1.5
0
1
2.5
箱数
1
4
2
3
2
8
(1)、在这20箱橘子中,最重的一箱比最轻的一箱重多少千克?(2)、与标准质量比较,20箱橘子总计超过或不足多少千克?(3)、若橘子每千克售价6.5元,则全部售完这20箱橘子共有多少元?22. 已知A=3a3-2ab+b2,B=-a3-ab+4b2(1)、求A-2B;(2)、当a、b满足(a+1)4+ =0时,求A-2B的值23. 如图,正方形ABCD的边长是a,正方形ECGF的边长是8.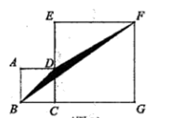 (1)、用含a的式子表示三角形BFG的面积(2)、用含a的式子表示阴影部分的面积,并求当a=4时,阴影部分的面积24. 如图,在数轴上点A表示数a,点B表示数b,点C表示数c,其中数b是最小的正整数,数a、c满足|a+2|+(c-6)2=0.若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.
(1)、用含a的式子表示三角形BFG的面积(2)、用含a的式子表示阴影部分的面积,并求当a=4时,阴影部分的面积24. 如图,在数轴上点A表示数a,点B表示数b,点C表示数c,其中数b是最小的正整数,数a、c满足|a+2|+(c-6)2=0.若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC. (1)、由题意可得:a= , b= , c=.(2)、若点A以每秒1个单位长度的速度沿数轴向左运动,点B和点C分别以每秒2个单位长度和3个单位长度的速度沿数轴向右运动,设点A、
(1)、由题意可得:a= , b= , c=.(2)、若点A以每秒1个单位长度的速度沿数轴向左运动,点B和点C分别以每秒2个单位长度和3个单位长度的速度沿数轴向右运动,设点A、B、C同时运动,运动时间为t秒.
①当t=2时,分别求A
C、AB的长度;
②在点A、
B、C同时运动的过程中,3AC-4AB的值是否随着时间t的变化而变化?若变化,说明理由;若不变,求出3AC-4AB的值.