2016-2017学年广西北海市合浦县八年级下学期期中数学试卷
试卷更新日期：2017-07-21 类型：期中考试
一、选择题
-
1. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列各组数是三角形的三边，能组成直角三角形的一组数是（ ）A、2，3，4 B、3，4，5 C、6，8，12 D、3. 如图，PD⊥AB，PE⊥AC，垂足分别为D、E，且PD=PE，则△APD与△APE全等的理由是（ ）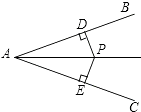
A、SAS B、AAS C、SSS D、HL4. 在▱ABCD中，如果∠A+∠C=140°，那么∠C等于（ ）A、20° B、40° C、60° D、70°5. 等边三角形的边长为2，则该三角形的面积为（ ）A、4 B、 C、2 D、36. 如果梯子的底端离建筑物5 米，13 米长的梯子可以达到该建筑物的高度是（ ）A、12 米 B、13 米 C、14 米 D、15 米7. 在▱ABCD中，∠A：∠B：∠C：∠D的值可以是（ ）A、1：2：2：1 B、1：2：3：4 C、2：1：1：2 D、2：1：2：18. 如果三角形的两条边分别为4和6，那么连结该三角形三边中点所得的周长可能是下列数据中的（ ）A、6 B、8 C、10 D、129. 下列性质中，矩形具有但平行四边形不一定具有的是（ ）A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分10. 已知如图，△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（ ）
A、315° B、270° C、180° D、135°11. 如图，点P是矩形ABCD的边AD上的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是（ ）
A、 B、 C、 D、不确定二、填空题
-
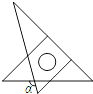
12. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是 ．13. 将一副直角三角板如图放置，使含30°角的三角板的一段直角边与含45°角的三角板的一段直角边重合，则∠α的度数为 ．
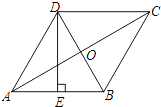
14. 如图，△ABC为等边三角形，DC∥AB，AD⊥CD于D．若△ABC的周长为 cm，则CD=cm．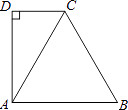
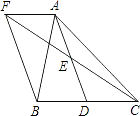
15. 如图，已知正方形ABCD的边长为4，对角线AC与BD相交于点O，点E在DC边的延长线上．若∠CAE=15°，则AE= ．
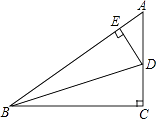
16. 如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是 ．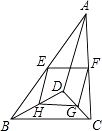
17. 如图，在△ABC中，∠A=90，BD是角平分线，若AD=m，BC=n，则△BDC的面积为 ．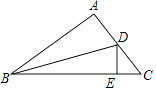
三、解答题
-
18. 如图，∠C=90°，AC=3，BC=4，AD=12，BD=13，试判断△ABD的形状，并说明理由．
19. 已知：如图，E，F是▱ABCD的对角线AC上的两点，BE∥DF，求证：AF=CE．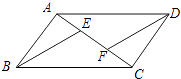
20.在4×3的网格上，由个数相同的白色方块与黑色方块组成一幅图案，请仿照此图案，在下列网格中分别设计出符合要求的图案（注：①不得与原图案相同；②黑、白方块的个数要相同）．
(1)、是轴对称图形，又是中心对称图形；
(2)、是轴对称图形，但不是中心对称图形；
(3)、是中心对称图形，但不是轴对称图形．
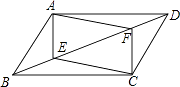
21. 如图，在▱ABCD中，BD为对角线，E、F是BD上的点，且BE=DF．求证：四边形AECF是平行四边形．
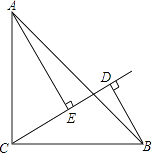
22. 如图，已知△ABC中，∠ACB=90°，且AC=BC．过点C作一条射线CE⊥AE于点E，再过点B作BD⊥CE于点D．试证明AE=BD+DE．
