2016-2017学年广东省广州市四校联考八年级下学期期中数学试卷

试卷更新日期：2017-07-21 类型：期中考试

进入出卷网下载

一、一.选择题

1. 式子 $\sqrt{x + 3}$ 有意义，则x的取值范围是（）

A、x≥3 B、x≤3 C、x≥﹣3 D、x≤﹣3

查看试题解析
2. 在△ABC中，三边长满足b²﹣a²=c² ，则互余的一对角是（）

A、∠A与∠B B、∠B与∠C C、∠A与∠C D、以上都不正确

查看试题解析
3. 一直角三角形两边分别为3和5，则第三边为（）

A、4 B、 $\sqrt{34}$ C、4或 $\sqrt{34}$ D、2

查看试题解析
4. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{0.5}$ B、 $\sqrt{4 a}$ C、 $\sqrt{8}$ D、 $\sqrt{10}$

查看试题解析
5. 如图，所有三角形都是直角三角形，所有四边形都是正方形，已知S₁=4，S₂=9，S₃=8，S₄=10，则S=（）

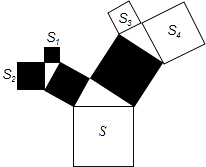A、25 B、31 C、32 D、40

查看试题解析
6. 在平行四边形ABCD中，∠A：∠B：∠C=2：3：2，则∠D=（　　）

A、36° B、108° C、72° D、60°

查看试题解析
7. 实数a，b在数轴上的位置如图所示，则化简 $\sqrt{{(a - 1)}^{2}}$ ﹣ $\sqrt{{(a - b)}^{2}}$ +b的结果是（）

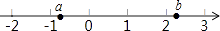A、1 B、b+1 C、2a D、1﹣2a

查看试题解析
8. 在△ABC中，∠ACB=90°，AC=40，CB=9，M、N在AB上且AM=AC，BN=BC，则MN的长为（）

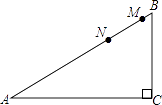A、6 B、7 C、8 D、9

查看试题解析
9. 下列命题中，真命题是（　　）.

A、对角线相等且互相垂直的四边形是菱形 B、有一条对角线平分对角的四边形是菱形 C、菱形是对角线互相垂直平分的四边形 D、菱形的对角线相等

查看试题解析
10. 下列命题：如图，正方形ABCD中，E、F分别为AB、AD上的点，AF=BE，CE、BF交于H，BF交AC于M，O为AC的中点，OB交CE于N，连OH．下列结论中：①BF⊥CE；②OM=ON；③ $O H = \frac{1}{2} C N$ ；④ $\sqrt{2} O H + B H = C H$ ．其中正确的命题有（）

A、只有①② B、只有①②④ C、只有①④ D、①②③④

查看试题解析

二、填空题

11. 2 $\sqrt{15}$ × $\sqrt{5}$ = ．

查看试题解析
12. m，n分别是 $\sqrt{2}$ ﹣1的整数部分和小数部分，则2m﹣n= ．

查看试题解析
13.
如图，台阶A处的蚂蚁要爬到B处搬运食物，它爬的最短距离是．

查看试题解析
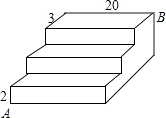14. 如图，在Rt△ABC中，∠C=90°，BC=3，AC=4，M为斜边AB上一动点，过M作MD⊥AC，过M作ME⊥CB于点E，则线段DE的最小值为．

查看试题解析
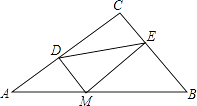15. 如图，矩形ABCD中，AB=15cm，点E在AD上，AE=9cm，连接EC，将矩形ABCD沿BE翻折，点A恰好落在EC上的点A′处，则BC=cm．

查看试题解析
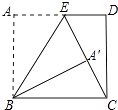16.
如图，在平面直角坐标系中，边长为1的正方形OA₁B₁C₁的两边在坐标轴上，以它的对角线OB₁为边作正方形OB₁B₂C₂ ，再以正方形OB₁B₂C₂的对角线OB₂为边作正方形OB₂B₃C₃ ，以此类推…、则正方形OB₂₀₁₅B₂₀₁₆C₂₀₁₆的顶点B₂₀₁₆的坐标是．

查看试题解析

三、解答题

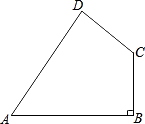
17. 计算：（ $\sqrt{5}$ ﹣2）²⁰¹⁴（ $\sqrt{5}$ +2）²⁰¹⁵﹣2|﹣ $\frac{\sqrt{5}}{2}$ |﹣（1﹣ $\sqrt{2}$ ）⁰ ．

查看试题解析
18. 先化简，再求值： $\frac{4 (x^{2} - x)}{x - 1}$ +（x﹣2）²﹣6 $\sqrt{\frac{x^{2}}{9}}$ ，其中，x= $\sqrt{5}$ +1．

查看试题解析
19. 如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°，求证：∠A+∠C=180°．

查看试题解析
20. 如图，将平行四边形ABCD的对角线BD向两个方向延长至点E和点F，使BE=DF，求证：四边形AECF是平行四边形．

查看试题解析
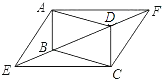21. 如图，点C在线段BD上，AC⊥BD，CA=CD，点E在线段CA上，且满足DE=AB，连接DE并延长交AB于点F．

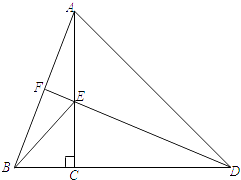(1)、求证：DE⊥AB；

(2)、若已知BC=a，AC=b，AB=c，设EF=x，则△ABD的面积用代数式可表示为；S_△_ABD= $\frac{1}{2}$ c（c+x）你能借助本题提供的图形，证明勾股定理吗？试一试吧．

查看试题解析
22. 如图，在菱形ABCD中，F是BC上任意一点，连接AF交对角线BD于点E，连接AF交对角线于点E，连接EC

(1)、求证：AE=EC；

(2)、当∠ABC=60°，∠CEF=60°时，点F在线段BC的什么位置？说明理由．

查看试题解析
23. 如图，已知四边形ABCD为正方形，AB= $2 \sqrt{2}$ ，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE．交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．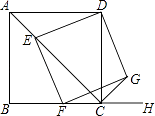
①求证：矩形DEFG是正方形；
②探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．

查看试题解析
24. 如图：在△ABC中，CE、CF分别平分∠ACB与它的邻补角∠ACD，AE⊥CE于E，AF⊥CF于F，直线EF分别交AB、AC于M、N．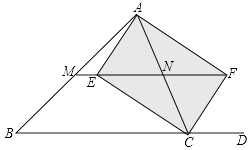

(1)、求证：四边形AECF为矩形；

(2)、试猜想MN与BC的关系，并证明你的猜想；

(3)、如果四边形AECF是菱形，试判断△ABC的形状，直接写出结果，不用说明理由．

查看试题解析
25.
如图，四边形OMTN中，OM=ON，TM=TN，我们把这种两组邻边分别相等的四边形叫做筝形．

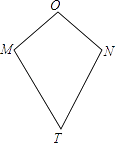(1)、探究筝形对角线之间的位置关系，并证明你的结论；

(2)、在筝形ABCD中，已知AB=AD=10，BC=CD，BC＞AB，BD、AC为对角线，BD=16．
①若∠ABC=90°，求AC的长；
②过点B作BF⊥CD于F，BF交AC于点E，连接DE．当四边形ABED为菱形时，求点F到AB的距离．

查看试题解析