2016-2017学年甘肃省定西市临洮县八年级下学期期中数学试卷

试卷更新日期：2017-07-21 类型：期中考试

进入出卷网下载

一、选择题

1. 要使式子 $\sqrt{x + 2}$ 有意义，则x的取值范围是（）

A、x＞0 B、x≥﹣2 C、x≥2 D、x≤2

查看试题解析
2. 下列运算中错误的是（）

A、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{6}$ B、 $\sqrt{8}$ ÷ $\sqrt{2}$ =2 C、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ D、（﹣ $\sqrt{3}$ ）²=3

查看试题解析
3. 下列根式中属最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{8}$ D、 $\sqrt{4 a + 4}$

查看试题解析
4. △ABC中，∠A、∠B、∠C的对边分别是a、b、c，AB=8，BC=15，CA=17，则下列结论不正确的是（）

A、△ABC是直角三角形，且AC为斜边 B、△ABC是直角三角形，且∠ABC=90° C、△ABC的面积是60 D、△ABC是直角三角形，且∠A=60°

查看试题解析
5. 如图，在菱形ABCD中，对角线AC、BD相交于点O，E为BC的中点，则下列式子中一定成立的是（）

A、AC=2OE B、BC=2OE C、AD=OE D、OB=OE

查看试题解析
6. 在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的条件是（）

A、AC=BD，AB∥CD，AB=CD B、AD∥BC，∠A=∠C C、AO=BO=CO=DO，AC⊥BD D、AO=CO，BO=DO，AB=BC

查看试题解析
7. 如图，在▱ABCD中，CE是∠DCB的平分线，F是AB的中点，AB=6，BC=5，则AE：EF：FB为（）

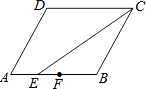A、1：2：3 B、2：1：3 C、3：2：1 D、3：1：2

查看试题解析
8. 在Rt△ABC中，∠C=90°，AC=3，BC=4，则点C到AB的距离是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{12}{5}$ D、 $\frac{3}{4}$

查看试题解析
9. 给出下列命题：
①在直角三角形ABC中，已知两边长为3和4，则第三边长为5；
②△ABC中，若∠A：∠B：∠C=1：5：6，则△ABC是直角三角形；
③三角形的三边a、b、c满足a²+c²=b² ，则△ABC是∠C为直角的直角三角形；
④△ABC中，若 a：b：c=1：2： $\sqrt{3}$ ，则这个三角形是直角三角形．
其中，正确命题的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 四边形的四边顺次为a、b、c、d，且满足a²+b²+c²+d²=2（ab+cd），则这个四边形一定是（）

A、平行四边形 B、两组对角分别相等的四边形 C、对角线互相垂直的四边形 D、对角线长相等的四边形

查看试题解析

二、填空题

11. 若一个长方体的长为 $2 \sqrt{6} c m$ ，宽为 $\sqrt{3} c m$ ，高为 $\sqrt{2} c m$ ，则它的体积为
cm³ ．

查看试题解析
12. 若 $\sqrt{m - 3} + {(n + 1)}^{2} = 0$ ，则m﹣n的值为．

查看试题解析
13. 等边三角形的边长为2，则该三角形的高为．

查看试题解析
14. 如图，以直角△ABC的三边向外作正方形，其面积分别为S₁ ， S₂ ， S₃且S₁=4，S₂=8，则S₃= ．

查看试题解析
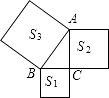
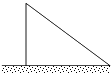
15. 如图，已知一根长8m的竹竿在离地3m处断裂，竹竿顶部抵着地面，此时，顶部距底部有 m．

查看试题解析
16. 直角三角形中，两直角边长分别为12和5，则斜边中线长是．

查看试题解析
17. 已知平行四边形ABCD的对角线AC，BD相交于点O，AB=4，AO=3，BO=5，则平行四边形面积是．

查看试题解析
18. 如图，O是矩形ABCD对角线的交点，AE平分∠BAD，∠AOD=120°，则∠AEO=
度．

查看试题解析

三、解答题

19. 如图，在数轴上画出表示 $\sqrt{17}$ 的点（不写作法，但要保留画图痕迹）．

查看试题解析
20. 计算：|﹣ $\frac{1}{2}$ |+ $\sqrt{{(- 2)}^{2}}$ + $\sqrt[3]{- 8}$ +（ $\sqrt{2}$ ）² ．

查看试题解析
21. 小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先画出了如图的四边形ABCD，并写出了如下不完整的已知和求证．

(1)、在方框中填空，以补全已知和求证；
已知：如图，在四边形ABCD中，BC=AD，．
求证：四边形ABCD是．

(2)、写出证明过程：

查看试题解析
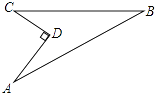
22. 如图所示，有一块地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，则这块地的面积．

查看试题解析
23. 已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．

(1)、求证：四边形DEFG是平行四边形；

(2)、如果△ABC中AB=AC，四边形DEFG的形状是（直接写出结果）．

查看试题解析
24. 如图，一架梯子的长度为15米，斜靠在墙上，梯子低部离墙底端为9米．

(1)、这个梯子顶端离地面有米；

(2)、如果梯子的底部沿水平方向向外滑动了4米，那么梯子的顶端下滑了几米？（结果用二次根式表示）

查看试题解析
25. 实践与探索

(1)、填空： $\sqrt{3^{2}}$ =； $\sqrt{{(- 5)}^{2}}$ =；

(2)、观察第（1）的结果填空：当a≥0时 $\sqrt{a^{2}}$ =；当a＜0时， $\sqrt{a^{2}}$ =；

(3)、利用你总结的规律计算： $\sqrt{{(x - 2)}^{2}}$ + $\sqrt{{(x - 3)}^{2}}$ ，其中2＜x＜3．

查看试题解析
26. 如图，在△ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°．

(1)、求∠BAC的度数．

(2)、若AD=2 $\sqrt{3}$ ，求AC和AB的长．

查看试题解析
27. 如图，已知点E是▱ABCD中BC边的中点，若∠ABE=∠BAE=60°，BC=4，连接AE并延长交DC的延长线于点F．

(1)、连接AC，BF，求证：四边形ABFC为矩形；

(2)、求四边形ABFC的周长和面积．

查看试题解析
28.
（在矩形ABCD中，AB=4，BC=8，经过对角线交点O的直线EF绕点O旋转，分别交AD、BC于点E、F，连接AF、CE．

(1)、如图（1），依据下列条件在普通四边形、梯形、普通平行四边形、矩菱形或正方形中选择填空：旋转过程中四边形AFCE始终为；
当点E为AD的中点时四边形AFCE为；
当EF⊥AC时四边形AFCE为；

(2)、如图（1），当EF⊥AC时，求AF的长；

(3)、如图（2），在（2）的基础上，若动点P从A点出发，沿A→F→B→A运动一周停止，速度为每秒5厘米；同时点Q从C点出发，沿C→D→E→C运动一周停止，速度为每秒4厘米，在P、Q运动过程中，第几秒时，四边形APCQ是平行四边形？

查看试题解析