2017年浙江省台州市临海市第三教研区中考数学模拟试卷

试卷更新日期：2017-07-21 类型：中考模拟

进入出卷网下载

一、选择题

1. $- \sqrt{3} + 1$
的倒数是（）

A、 $- \frac{\sqrt{3} - 1}{2}$ B、 $\frac{\sqrt{3} + 1}{2}$ C、 $- \frac{1 + \sqrt{3}}{2}$ D、 $- \frac{1 - \sqrt{3}}{2}$

查看试题解析
2. 一个几何体的三视图如图所示，则该几何体表面积为（）

A、3π B、5π C、6π D、8π

查看试题解析
3. 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法表示为（）

A、6.75×10³吨 B、6.75×10^﹣⁴吨 C、6.75×10⁵吨 D、6.75×10⁴吨

查看试题解析
4.
如图，已知一商场自动扶梯的长l为13米，高度h为5米，自动扶梯与地面所成的夹角为θ，则tanθ的值等于（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
5. 关于x的不等式组 ${\begin{matrix} \frac{x + 15}{2} > x - 3 \\ \frac{2 x + 2}{3} < x + a \end{matrix}$ 只有5个整数解，则a的取值范围是（）

A、﹣ $\frac{14}{3}$ ≤a≤﹣ $\frac{13}{3}$ B、﹣ $\frac{14}{3}$ ≤a＜﹣ $\frac{13}{3}$ C、﹣ $\frac{14}{3}$ ＜a＜﹣ $\frac{13}{3}$ D、﹣ $\frac{14}{3}$ ＜a≤﹣ $\frac{13}{3}$

查看试题解析
6. 如果将抛物线y=x²+2向右平移1个单位，那么所得新抛物线的表达式是（）

A、y=x²+3 B、y=（x﹣1）²+2 C、y=（x+1）²+2 D、y=x²+1

查看试题解析
7.
如图，在△ABC中，∠BAC=50°，把△ABC沿EF折叠，C对应点恰好与△ABC的外心O重合，则∠CFE的度数是（　　）

A、40° B、45° C、50° D、55°

查看试题解析
8. 定义新运算：对于任意实数a、b都有a⊗b=|3a﹣b|，则x⊗1﹣x⊗2的值为（）

A、﹣2 B、﹣1 C、﹣ $\frac{3}{2}$ D、0

查看试题解析
9. 若m是一元二次方程x²﹣5x﹣2=0的一个实数根，则2014﹣m²+5m的值是（）

A、2011 B、2012 C、2013 D、2014

查看试题解析
10. 如图，在菱形ABCD中，对角线AC、BD交于点O，以OB为直径画圆M，过D作⊙M的切线，切点为N，分别交AC、BC于点E、F，已知AE=5，CE=3，则DF的长是（）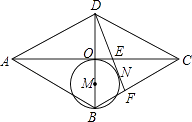

A、3 B、4 C、4.8 D、5

查看试题解析

二、填空题

11. 计算：cos²60°= ．

查看试题解析
12. 一次函数y₁=﹣x+2，反比例函数y₂= $- \frac{8}{x}$ ，当y₁＜y₂时，x的取值范围．

查看试题解析
13. 如图，点D为∠BAC边AC上一点，点O为边AB上一点，AD=DO．以O为圆心，OD长为半径作半圆，交AC于另一点E，交AB于点F、G，连接EF．若∠BAC=22°，则∠EFG=°．

查看试题解析
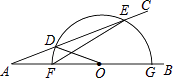14. 如图是一个古代车轮的碎片，小明为求其外圆半径，连结外圆上的两点A、B，并使AB与车轮内圆相切于点D，做CD⊥AB交外圆于点C．测得CD=10cm，AB=60cm，则这个车轮的外圆半径为cm．

查看试题解析
15. 如图，△ABC中，∠A的平分线交BC于D，若AB=6cm，AC=4cm，∠A=60°，则AD的长为cm．

查看试题解析
16.
如图，在等腰△ABC中，AB=AC=5，BC=6，AD⊥BC于点D，动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动，过点P作PE⊥AB于点E，过点P作PF∥BA，交AC于点F，设点P运动的时间为t秒．若以PE所在的直线为对称轴，线段BD经轴对称变换后的图形为B'D'，求当线段B'D'与线段AC有交点这段过程中，线段B'D'扫过的面积．

查看试题解析

三、解答题

17. 综合题。

(1)、计算：（π﹣3.14）⁰+（ $\frac{1}{2}$ ）^﹣¹+|﹣2 $\sqrt{2}$ |﹣ $\sqrt{8}$ ．

(2)、先化简，再求值： $\frac{2 x - 6}{x^{2} + 2 x + 1}$ ÷（ $\frac{x^{2} + 1}{x + 1}$ ﹣x+1），并从﹣tan60°≤x≤2cos30°取出一个合适的整数，求出式子的值．

查看试题解析
18. 已知直线PD垂直平分⊙O的半径OA于点B，PD交⊙O于点C、D，PE是⊙O的切线，E为切点，连结AE，交CD于点F．

(1)、若⊙O的半径为8，求CD的长；

(2)、证明：PE=PF；

(3)、若PF=13，sinA= $\frac{5}{13}$ ，求EF的长．

查看试题解析
19.
如图是由边长为1的小正三角形组成的网格图，点O和△ABC的顶点都在正三角形的格点上，将△ABC绕点O逆时针旋转120°得到△A′B′C′．

(1)、在网格中画出旋转后的△A′B′C′；

(2)、求AB边旋转时扫过的面积．

查看试题解析
20.
如图，AB、CD是两个过江电缆的铁塔，塔AB高40米，AB的中点为P，塔底B距江面的垂直高度为6米．跨江电缆因重力自然下垂近似成抛物线形，为了保证过往船只的安全，电缆下垂的最低点距江面的高度不得少于30米．已知：人在距塔底B点西50米的地面E点恰好看到点E、P、C在一直线上；再向西前进150米后从地面F点恰好看到点F、A、C在一直线上．

(1)、求两铁塔轴线间的距离（即直线AB、CD间的距离）；

(2)、若以点A为坐标原点，向东的水平方向为x轴，取单位长度为1米，BA的延长方向为y轴建立坐标系．求刚好满足最低高度要求的这个抛物线的解析式．

查看试题解析
21. 临海市初中第三教研区为了丰富学生课余活动，组织同学开展每周一次的社团活动，活动内容有足球、跳绳、跳舞、篮球、象棋共5项，为方便组织，规定每位同学只能报一项活动，根据报名绘制了如下两幅尚不完整的统计图，解答下列问题：

(1)、将条形统计图补充完整；

(2)、写出扇形统计图中的m和n的值；

(3)、瑶瑶和欣欣两名同学对足球、篮球、象棋三项活动都很感兴趣，决定从三项活动中随机抽取一项参加，利用树状图或列表表示所有可能结果，并求出两人参加同一项目的概率；

(4)、由于场地限制，参加足球活动的学生人数不能超过参加其余活动学生人数的 $\frac{1}{6}$ ，那么至少几位同学需要从参加足球活动调整到参加其余活动？

查看试题解析
22. 某花木公司在20天内销售一批马蹄莲．其中，该公司的鲜花批发部日销售量y₁（万朵）与时间x（x为整数，单位：天）部分对应值如下表所示．
时间x（天）
0
4
8
12
16
20
销量y₁（万朵）
0
16
24
24
16
0
另一部分鲜花在淘宝网销售，网上销售日销售量y₂（万朵）与时间x（x为整数，单位：天）关系如图所示．

(1)、请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y₁与x的变化规律，写出y₁与x的函数关系式及自变量x的取值范围；

(2)、观察马蹄莲网上销售量y₂与时间x的变化规律，请你设想商家采用了何种销售策略使得销售量发生了变化，并写出销售量y₂与x的函数关系式及自变量x的取值范围；

(3)、设该花木公司日销售总量为y万朵，写出y与时间x的函数关系式，并判断第几天日销售总量y最大，并求出此时最大值．

查看试题解析
23.
如图（1），在平面直角坐标系中，矩形ABCO，B点坐标为（4，3），抛物线y= $- \frac{1}{2}$ x²+bx+c经过矩形ABCO的顶点B、C，D为BC的中点，直线AD与y轴交于E点，与抛物线y= $- \frac{1}{2}$ x²+bx+c交于第四象限的F点．

(1)、求该抛物线解析式与F点坐标；

(2)、
如图（2），动点P从点C出发，沿线段CB以每秒1个单位长度的速度向终点B运动；同时，动点M从点A出发，沿线段AE以每秒 $\frac{\sqrt{13}}{2}$ 个单位长度的速度向终点E运动．过点P作PH⊥OA，垂足为H，连接MP，MH．设点P的运动时间为t秒

①问EP+PH+HF是否有最小值？如果有，求出t的值；如果没有，请说明理由．
②若△PMH是等腰三角形，请直接写出此时t的值．

查看试题解析
24. 新定义函数：在y关于x的函数中，若0≤x≤1时，函数y有最大值和最小值，分别记y_max和y_min ，且满足 ${\begin{matrix} y_{m i n} > 0 \\ 2 y_{m i n} > y_{m a x} \end{matrix}$ ，则我们称函数y为“三角形函数”．

(1)、若函数y=x+a为“三角形函数”，求a的取值范围；

(2)、判断函数y=x²﹣ $\frac{\sqrt{2}}{2}$ x+1是否为“三角形函数”，并说明理由；

(3)、已知函数y=x²﹣2mx+1，若对于0≤x≤1上的任意三个实数a，b，c所对应的三个函数值都能构成一个三角形的三边长，则求满足条件的m的取值范围．

查看试题解析

时间x（天）	0	4	8	12	16	20
销量y₁（万朵）	0	16	24	24	16	0