2017年浙江省宁波市江北区中考数学模拟试卷（4月份）

试卷更新日期：2017-07-21 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的绝对值是（）

A、﹣2 B、2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 下列运算正确的是（）

A、a+a²=a³ B、（3a）²=6a² C、a⁶÷a²=a³ D、a•a³=a⁴

查看试题解析
3. 宁波奥林匹克体育中心坐落于江北区，一期“三馆一圆”总投资35亿元，其中35亿元用科学记数法表示为（）

A、0.35×10¹⁰元 B、3.5×10⁸元 C、3.5×10⁹元 D、35×10⁸元

查看试题解析
4. 如图是由4个大小相同的正方体搭成的几何体，其俯视图是（）

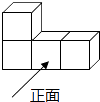A、 B、 C、 D、

查看试题解析
5. 若二次根式 $\sqrt{x - 4}$ 有意义，则x的取值范围是（）

A、x＞4 B、x≥4 C、x≤4 D、x≠4

查看试题解析
6. 一个不透明的布袋里装有6个黑球和3个白球，它们除颜色外其余都相同，从中任意摸出一个球，是白球的概率为（）

A、 $\frac{1}{9}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
7. 有一副七巧板如图所示，其中三个阴影部分的面积分别为S₁ ， S₂ ， S₃ ，则S₁：S₂：S₃=（）

A、1：2：3 B、1： $\sqrt{2}$ ：2 C、1： $\sqrt{2}$ ：4 D、1：2：4

查看试题解析
8.
如图是某市2016年四月每日的最低气温（℃）的统计图，则在四月份每日的最低气温这组数据中，中位数和众数分别是（）

A、14℃，14℃ B、15℃，15℃ C、14℃，15℃ D、15℃，14℃

查看试题解析
9. 已知圆形纸片⊙O的直径为2，将其沿着两条互相垂直的直径折叠，得到四层的扇形，将最上的一层“撑”开来，“鼓”成一个无底的圆锥，则这个圆锥的高是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
10. 如图，一场篮球赛中，篮球运动员跳起投篮，已知球出手时离地面高2.2m，与篮圈中心的水平距离为8m，当球出手后水平距离为4m时达到最大高度4m，篮圈运行的轨迹为抛物线的一部分，篮圈中心距离地面3m，运动员发现未投中，若假设出手的角度和力度都不变，要使此球恰好通过篮圈中心，运动员应该跳得（）

A、比开始高0.8m B、比开始高0.4m C、比开始低0.8m D、比开始低0.4m

查看试题解析
11.
如图，在矩形ABCD内放入六个小正方形后形成一个中心对称图形，其中顶点E、F分别在边BC、AD上，则长AD与宽AB的比值为（）

A、6：5 B、13：10 C、8：7 D、4：3

查看试题解析
12. 如图，曲线AB是顶点为B，与y轴交于点A的抛物线y=﹣x²+4x+2的一部分，曲线BC是双曲线y= $\frac{k}{x}$ 的一部分，由点C开始不断重复“A﹣B﹣C”的过程，形成一组波浪线，点P（2017，m）与Q（2025，n）均在该波浪线上，过点P、Q分别作x轴的垂线，垂足为M、N，连结PQ，则四边形PMNQ的面积为（）

A、72 B、36 C、16 D、9

查看试题解析

二、填空题

13. 实数4的算术平方根是．

查看试题解析
14. 分解因式：x²y﹣y= ．

查看试题解析
15. 在Rt△ABC中，∠C=90°，若sinA= $\frac{3}{4}$ ，则cosB= ．

查看试题解析
16. 若（a﹣2）²﹣1=0，则5+8a﹣2a²的值为．

查看试题解析
17. 有一玻璃密封器皿如图①，测得其底面直径为20cm，高20cm，现内装蓝色溶液若干．如图②放置时，测得液面高10cm；如图③放置时，测得液面高16cm；则该玻璃密封器皿总容量为cm³（结果保留π）

查看试题解析
18. 如图，已知反比例函数y=﹣ $\frac{1}{x}$ 的图象与直线y=kx（k＜0）相交于点A、B，以AB为底作等腰三角形，使∠ACB=120°，且点C的位置随着k的不同取值而发生变化，但点C始终在某一函数图象上，则这个图象所对应的函数解析式为．

查看试题解析

三、解答题

19. 计算：（﹣1）²⁰¹⁷﹣ $\sqrt[3]{8}$ +（﹣2017）⁰+tan45°．

查看试题解析
20. 解方程： $\frac{x - 3}{x - 2} + 1 = \frac{3}{2 - x}$ ．

查看试题解析
21.
某校以“我最想去的社会实践地”为课题，开展了一次调查，从全校同学中随机抽取了部分同学进行调查，每位同学从“荪湖花海”、“保国寺”、“慈城古镇”、“绿色学校”中选取一项最想去的社会实践地，并将调查结果绘制成如下的统计图（部分信息未给出）．
请根据统计图中信息，解答下列问题：

(1)、该调查的样本容量为， a=%，b=%，“荪湖花海”所对应扇形的圆心角度数为度．

(2)、补全条形统计图；

(3)、若该校共有1600名学生，请估计全校最想去“绿色学校”的学生共有多少名？

查看试题解析
22. 如图，已知图①中抛物线y=ax²+bx+c经过点D（﹣1，0）、C（0，﹣1）、E（1，0）．

(1)、求图①中抛物线的函数表达式；

(2)、将图①中抛物线向上平移一个单位，再绕原点O顺时针旋转180°后得到图②中抛物线，则图②中抛物线的函数表达式为；

(3)、图②中抛物线与直线y=﹣ $\frac{1}{2}$ x﹣ $\frac{1}{2}$ 相交于A、B两点（点A在点B的左侧），如图③，求点A、B的坐标，并直接写出当一次函数的值大于二次函数的值时，x的取值范围．

查看试题解析
23. 如图①，AE是⊙O的直径，点C是⊙O上的点，连结AC并延长AC至点D，使CD=CA，连结ED交⊙O于点B．

(1)、求证：点C是劣弧 $\hat{A B}$ 的中点；

(2)、如图②，连结EC，若AE=2AC=4，求阴影部分的面积．

查看试题解析
24. 图中的网格称之为三角形网格，它的每一个小三角形都是边长为1的正三角形，画出格点△ABC（即△ABC三个顶点都在小正三角形的顶点处），如图所示，请按照下列要求，画出相应的图形，并计算．

(1)、请在①中画出一个与△ABC面积相等，且不全等的格点三角形，并写出相应的面积；

(2)、请在图②和图③中分别画出一个与△ABC相似，且互补全等的格点三角形，并写出相应的相似比k（△ABC与△A′B′C′之比）

查看试题解析
25. A、B两城由笔直的铁路连接，动车甲从A向B匀速前行，同时动车乙从B向A匀速前行，到达目的地时停止，其中动车乙速度较快，设甲乙两车相距y（km），甲行驶的时间为t（h），y关于t的函数图象如图所示．

(1)、填空：动车甲的速度为（km/h），动车乙的速度为（km/h）；

(2)、求图中点P的坐标，并解释该点坐标所表示的实际意义；

(3)、两车何时相距1200km？

查看试题解析
26. 定义：一个矩形的两邻边之比为 $\sqrt{3}$ ，则称该矩形为“特比矩形”．

(1)、如图①，在“特比矩形”ABCD中， $\frac{A B}{B C}$ = $\sqrt{3}$ ，求∠AOD的度数；

(2)、如图②，特比矩形CDEF的边CD在半圆O的直径AB上，顶点E、F在半圆上，已知直径AB= $\sqrt{7}$ ，求矩形CDEF的面积；

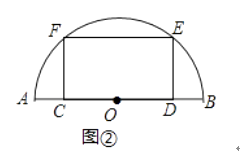(3)、在平面直角坐标系xOy中，⊙O的半径为 $\sqrt{3}$ ，点Q的坐标为（q，2 $\sqrt{3}$ ），如果在⊙O上存在一点P，过点P作x轴的垂线与过点Q作y轴的垂线交于点M，过点P作y轴的垂线与过点Q作x轴的垂线交于点N，以点P、Q、M、N为顶点的矩形是“特比矩形”，请直接写出q的取值范围．

查看试题解析
27. 如图①，在△ABC中，∠ACB=90°，AC=BC= $\sqrt{2}$ ，D、E是AB边上的两个动点，满足∠DCE=45°．

(1)、如图②，把△ADC绕着点C顺时针旋转90°，得到△BKC，连结EK．
①求证：△DCE≌△KCE．
②求证：DE²=AD²+BE² ．
③思考与探究：当点D从点A向AB的中点运动的过程中，请尝试写出DE长度的变化趋势 $\underline{}$ ；并直接写出DE长度的最大值或最小值 $\underline{}$ （标明最大值或最小值）．

(2)、如图③，若△CDE的外接圆⊙O分别交AC，BC于点F、G，求证：CF：CG=BE：AD．

查看试题解析