2017年浙江省杭州市滨江区中考数学一模试卷
试卷更新日期:2017-07-21 类型:中考模拟
一、选择题
-
1. 计算 ﹣ ×3的结果是( )A、0 B、1 C、﹣2 D、﹣12. 据统计,2017年春节黄金周7天,杭州共接待中外游客约450万人次,将450万用科学记数法表示,以下表示正确的是( )A、450×104 B、45.0×105 C、4.50×106 D、4.50×1073. 由六个相同的立方体搭成的几何体如图所示,下面有关它的三个视图的说法正确的是( )
 A、左视图与主视图相同 B、俯视图与主视图相同 C、左视图与俯视图相同 D、三个视图都相同4. 如图,AB∥CD,AD与BC相交于点E,若∠A=40°,∠C=35°,则∠BED=( )
A、左视图与主视图相同 B、俯视图与主视图相同 C、左视图与俯视图相同 D、三个视图都相同4. 如图,AB∥CD,AD与BC相交于点E,若∠A=40°,∠C=35°,则∠BED=( ) A、70° B、75° C、80° D、85°5. 下列计算正确的是( )A、x4+x2=x6 B、(a+b)2=a2+b2 C、(3x2y)2=6x4y2 D、(﹣m)7÷(﹣m)2=﹣m56. 下列命题中,真命题是( )A、垂直于同一条直线的两条直线互相平行 B、平分弦的直径垂直弦 C、有两边及一角对应相等的两个三角形全等 D、八边形的内角和是外角和的3倍7. 某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是( )A、18(42﹣x)=12x B、2×18(42﹣x)=12x C、18(42﹣x)=2×12x D、18(21﹣x)=12x8. 某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
A、70° B、75° C、80° D、85°5. 下列计算正确的是( )A、x4+x2=x6 B、(a+b)2=a2+b2 C、(3x2y)2=6x4y2 D、(﹣m)7÷(﹣m)2=﹣m56. 下列命题中,真命题是( )A、垂直于同一条直线的两条直线互相平行 B、平分弦的直径垂直弦 C、有两边及一角对应相等的两个三角形全等 D、八边形的内角和是外角和的3倍7. 某校社团活动课中,手工制作社的同学用一种彩色硬纸板制作某种长方体小礼品的包装盒,每张硬纸板可制作盒身12个,或制作盒底18个,1个盒身与2个盒底配成一套,现有42张这种彩色硬纸板,要使盒身和盒底刚好配套,若设需用x张做盒身,则下面所列方程正确的是( )A、18(42﹣x)=12x B、2×18(42﹣x)=12x C、18(42﹣x)=2×12x D、18(21﹣x)=12x8. 某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)选修课
A
B
C
D
E
F
人数
20
30
根据图标提供的信息,下列结论错误的是( )
 A、这次被调查的学生人数为200人 B、扇形统计图中E部分扇形的圆心角为72° C、被调查的学生中最想选F的人数为35人 D、被调查的学生中最想选D的有55人9. 如图,在反比例函数y= (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( )
A、这次被调查的学生人数为200人 B、扇形统计图中E部分扇形的圆心角为72° C、被调查的学生中最想选F的人数为35人 D、被调查的学生中最想选D的有55人9. 如图,在反比例函数y= (x>0)的图象上有点P1、P2、P3、P4 , P5 , 它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , S4 , 则S1+S2+S3+S4的值为( ) A、4.5 B、4.2 C、4 D、3.810. 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
A、4.5 B、4.2 C、4 D、3.810. 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )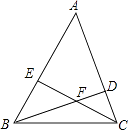 A、20 B、25 C、30 D、40
A、20 B、25 C、30 D、40二、填空题
-
11. 分解因式:m2﹣9=.
12. 如图,四个完全相同的小球上分别写有:0, ,﹣5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为 . 13. 不等式组 的最大整数解为 .14. 如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA的度数为度.
13. 不等式组 的最大整数解为 .14. 如图,点A,B,C都在⊙O上,若∠OAC=17°,∠ACB=46°,AC与OB交于点D,则∠ODA的度数为度. 15. 在矩形ABCD中,∠ABC的平分线交AD于点E,∠BED的平分线交DC于点F,若AB=6,点F恰为DC的中点,则BC=(结果保留根号)16. 已知二次函数y=ax2﹣bx+2(a≠0)图象的顶点在第二象限,且过点(1,0),则a的取值范围是;若a+b的值为非零整数,则b的值为 .
15. 在矩形ABCD中,∠ABC的平分线交AD于点E,∠BED的平分线交DC于点F,若AB=6,点F恰为DC的中点,则BC=(结果保留根号)16. 已知二次函数y=ax2﹣bx+2(a≠0)图象的顶点在第二象限,且过点(1,0),则a的取值范围是;若a+b的值为非零整数,则b的值为 .三、解答题
-
17. 先化简,再求值: + ,其中a=﹣5.18.
乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
 (1)、若乐乐这个月平均每天健步走的步数为1.32万步,试求她走1.3万步和1.5万步的天数;(2)、求这组数据中的众数和中位数.19. 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC.
(1)、若乐乐这个月平均每天健步走的步数为1.32万步,试求她走1.3万步和1.5万步的天数;(2)、求这组数据中的众数和中位数.19. 如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC. (1)、求证:△BDE≌△ADC;(2)、若BC=8.4,tanC= ,求DE的长.20.
(1)、求证:△BDE≌△ADC;(2)、若BC=8.4,tanC= ,求DE的长.20.如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.
 (1)、求这条直线的函数表达式;(2)、Rt△ABC与直线l在同一个平面直角坐标系内,其中∠ABC=90°,AC=2 ,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.21.
(1)、求这条直线的函数表达式;(2)、Rt△ABC与直线l在同一个平面直角坐标系内,其中∠ABC=90°,AC=2 ,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.21.如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
 (1)、求每个小矩形的长与宽;(2)、在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)(3)、求sin∠ACB的值.22. 设抛物线y=mx2﹣2mx+3(m≠0)与x轴交于点A(a,0)和B(b,0).(1)、若a=﹣1,求m,b的值;(2)、若2m+n=3,求证:抛物线的顶点在直线y=mx+n上;(3)、抛物线上有两点P(x1 , p)和Q(x2 , q),若x1<1<x2 , 且x1+x2>2,试比较p与q的大小.23. 综合题(1)、如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论;
(1)、求每个小矩形的长与宽;(2)、在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)(3)、求sin∠ACB的值.22. 设抛物线y=mx2﹣2mx+3(m≠0)与x轴交于点A(a,0)和B(b,0).(1)、若a=﹣1,求m,b的值;(2)、若2m+n=3,求证:抛物线的顶点在直线y=mx+n上;(3)、抛物线上有两点P(x1 , p)和Q(x2 , q),若x1<1<x2 , 且x1+x2>2,试比较p与q的大小.23. 综合题(1)、如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE﹣BF=EF,请证明这个结论;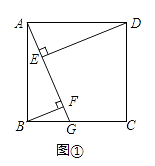 (2)、若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系;
(2)、若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系; (3)、如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由
(3)、如图③,四边形ABCD内接于⊙O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由