2017年云南省红河州个旧市中考数学一模试卷

试卷更新日期：2017-07-21 类型：中考模拟

进入出卷网下载

一、填空题

1. 某市户籍人口为1694000人，则该市户籍人口数据用科学记数法可表示为．

查看试题解析
2. 化简： $\frac{x^{2}}{x - 2} + \frac{4}{2 - x}$ = ．

查看试题解析
3. 关于x的一元二次方程（k﹣1）x²﹣2x+1=0有两个不相等的实数根，则实数k的取值范围是．

查看试题解析
4. 如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE= ．

查看试题解析
5. 在平面直角坐标系中，小明做走棋的游戏，其走法是：棋子从原点出发，第1步向右走1个单位，第2步向右走2个单位，第3步向上走1个单位，第4步向右走1个单位…依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位；当n被3除，余数为1时，则向右走1个单位；当n被3除，余数为2时，则向右走2个单位，当走完第100步时，棋子所处位置的坐标是．

查看试题解析

二、选择题

6. 9的相反数是（）

A、 $\frac{1}{9}$ B、9 C、﹣9 D、﹣ $\frac{1}{9}$

查看试题解析
7. 下列计算正确的是（　　）

A、2a²+4a²=6a⁴ B、（a+1）²=a²+1 C、（a²）³=a⁵ D、x⁷÷x⁵=x²

查看试题解析
8. 如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

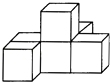A、 B、 C、 D、

查看试题解析
9. 下列说法正确的是（）

A、了解某班同学的身高情况适合用全面调查 B、数据2、3、4、2、3的众数是2 C、数据4、5、5、6、0的平均数是5 D、甲、乙两组数据的平均数相同，方差分别是S_甲²=3.2，S_乙²=2.9，则甲组数据更稳定

查看试题解析
10.
如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应54°，则∠BCD的度数为（　　）

A、27° B、54° C、63° D、36°

查看试题解析
11. 某校用420元钱到商场去购买“84”消毒液，经过还价，每瓶便宜0.5元，结果比用原价多买了20瓶，求原价每瓶多少元？设原价每瓶x元，则可列出方程为（）

A、 $\frac{420}{x}$ ﹣ $\frac{420}{x - 0.5}$ =20 B、 $\frac{420}{x - 0.5}$ ﹣ $\frac{420}{x}$ =20 C、 $\frac{420}{x}$ ﹣ $\frac{420}{x - 20}$ =0.5 D、 $\frac{420}{x - 20}$ ﹣ $\frac{420}{x}$ =0.5

查看试题解析
12. 如图，沿一条母线将圆锥侧面剪开并展开，得到一个扇形，若圆锥底面半径r=2，扇形圆心角θ=120°，则该圆锥母线长为（）

A、10 B、 $\frac{15}{2}$ C、6 D、8

查看试题解析
13. 如图，直线y=﹣x+3与y轴交于点A，与反比例函数y= $\frac{k}{x}$ （k≠0）的图象交于点C，过点C作CB⊥x轴于点B，AO=3BO，则反比例函数的解析式为（）

A、y= $\frac{2}{x}$ B、y=﹣ $\frac{2}{x}$ C、y= $\frac{4}{x}$ D、y=﹣ $\frac{4}{x}$

查看试题解析

三、解答题

14. 计算：（﹣ $\frac{1}{2}$ ）^﹣²+（ $\sqrt{2} -$ 1.414）⁰﹣3tan30°﹣ $\sqrt{{(- 2)}^{2}}$ ．

查看试题解析
15. 如图，在平行四边形ABCD中，E是AD边上的中点，连接BE，并延长BE交CD的延长线于点F．证明：FD=AB．

查看试题解析
16. 如图，在▱ABCD中，对角线AC与BD相交于点O，∠CAB=∠ACB，过点B作BE⊥AB交AC于点E．

(1)、求证：AC⊥BD；

(2)、若AB=14，cos∠CAB= $\frac{7}{8}$ ，求线段OE的长．

查看试题解析
17. 某社区为了进一步提高居民珍惜谁、保护水和水忧患意识，提倡节约用水，从本社区5000户家庭中随机抽取100户，调查他们家庭每季度的平均用水量，并将调查的结果绘制成如下的两幅不完整的统计图和表：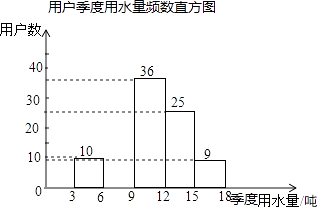
用户季度用水量频数分布表
平均用水量（吨）
频数
频率
3＜x≤6
10
0.1
6＜x≤9
m
0.2
9＜x≤12
36
0.36
12＜x≤15
25
n
15＜x≤18
9
0.09
请根据上面的统计图表，解答下列问题：

(1)、在频数分布表中：m= ， n=；

(2)、根据题中数据补全频数直方图；

(3)、如果自来水公司将基本季度水量定为每户每季度9吨，不超过基本季度用水量的部分享受基本价格，超出基本季度用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格？

查看试题解析
18. 某中学现要从两位男生和两位女生中，选派两位同学分别作为1号选手和2号选手代表学校参加汉字听写大赛．

(1)、请用树形图或列表法列举出所有可能选派的结果；

(2)、求恰好选派一男一女两位同学参赛的概率．

查看试题解析
19. 为了抓住2017年六一儿童节的商机，某商场决定购进甲、乙两种玩具进行销售，若购进甲种玩具1件，乙种玩具2件，需要160元，购进甲种玩具2件，乙种玩具3件，需要280元，购进甲、乙两种玩具每件各需要多少元？

查看试题解析
20. 如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=∠BFD．

(1)、求证：FD是⊙O的一条切线；

(2)、若AB=10，AC=8，求DF的长．

查看试题解析
21. 某地生产椪柑，春节期间，一外地运销客户安排15辆汽车装运A，B，C三种不同品质的椪柑120吨到外地销售，按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑，每种椪柑所用车辆都不少于3辆．

(1)、设装运A种椪柑的车辆数为x辆，装运B种椪柑车辆数为y辆，根据下表提供的信息，求出y与x之间的函数关系式；
椪柑品种
A
B
C
每辆汽车运载量（吨）
10
8
6

(2)、在（1）条件下，求出该函数自变量x的取值范围，车辆的安排方案共有几种？请写出每种安排方案．

查看试题解析
22.
如图，长方形OABC的OA边在x轴的正半轴上，OC在y轴的正半轴上，抛物线y=ax²+bx经过点B（1，4）和点E（3，0）两点．

(1)、求抛物线的解析式；

(2)、若点D在线段OC上，且BD⊥DE，BD=DE，求D点的坐标；

(3)、在条件（2）下，在抛物线的对称轴上找一点M，使得△BDM的周长为最小，并求△BDM周长的最小值及此时点M的坐标．

查看试题解析

平均用水量（吨）	频数	频率
3＜x≤6	10	0.1
6＜x≤9	m	0.2
9＜x≤12	36	0.36
12＜x≤15	25	n
15＜x≤18	9	0.09

椪柑品种	A	B	C
每辆汽车运载量（吨）	10	8	6