2017年天津市河东区中考数学一模试卷

试卷更新日期：2017-07-21 类型：中考模拟

进入出卷网下载

一、选择题：

1. 计算（﹣2）﹣5的结果等于（）

A、﹣7 B、﹣3 C、3 D、7

查看试题解析
2. tan60°的值等于（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
3.
如图是我国几家银行的标志，其中即是轴对称图形又是中心对称图形的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 国家统计局的相关数据显示，2015年我国国民生产总值（GDP）约为67670000000000元，将67670000000000用科学记数法表示为（）

A、6.767×10¹³ B、6.767×10¹² C、67.67×10¹² D、6.767×10¹⁴

查看试题解析
5. 如图，是由两个相同的小正方体和一个圆锥体组成的立体图形，其俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{19}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
7. 计算 $\frac{b}{a - b} + \frac{a}{b - a}$ 的结果是（）

A、a﹣b B、b﹣a C、1 D、﹣1

查看试题解析
8. 方程2（2x+1）（x﹣3）=0的两根分别为（）

A、 $\frac{1}{2}$ 和3 B、﹣ $\frac{1}{2}$ 和3 C、 $\frac{1}{2}$ 和﹣3 D、﹣ $\frac{1}{2}$ 和﹣3

查看试题解析
9. 如果点A、B、C、D所对应的数为a、b、c、d，则a、b、c、d的大小关系是（）

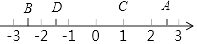A、a＜c＜d＜b B、b＜d＜a＜c C、b＜d＜c＜a D、d＜b＜c＜a

查看试题解析
10. 如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α（0°＜α＜90°）．若∠1=112°，则∠α的大小是（）

A、68° B、20° C、28° D、22°

查看试题解析
11. 若M（ $- \frac{1}{2}$ ，y₁）、N（ $- \frac{1}{4}$ ，y₂）、P（ $\frac{1}{2}$ ，y₃）三点都在函数 $y = \frac{k}{x}$ （k＞0）的图象上，则y₁、y₂、y₃的大小关系是（）

A、y₂＞y₃＞y₁ B、y₂＞y₁＞y₃ C、y₃＞y₁＞y₂ D、y₃＞y₂＞y₁

查看试题解析
12. 如图是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：
①a﹣b+c＞0；
②3a+b=0；
③b²=4a（c﹣n）；
④一元二次方程ax²+bx+c=n﹣1有两个互异实根．
其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 2x³•（﹣x²）= ．

查看试题解析
14. 计算 ${(2 \sqrt{3} + 3 \sqrt{2})}^{2}$ = ．

查看试题解析
15. 一枚质地匀均的骰子，其六个面上分别标有数字：1，2，3，4，5，6，投掷一次，朝上一面的数字是偶数的概率是．

查看试题解析
16. 一次函数y=（m﹣3）x﹣2的图象经过二、三、四象限，则m的取值范围是．

查看试题解析
17. 如图，正方形ABCD中，点E、F分别为AB、CD上的点，且AE=CF= $\frac{1}{3}$ AB，点O为线段EF的中点，过点O作直线与正方形的一组对边分别交于P、Q两点，并且满足PQ=EF，则这样的直线PQ（不同于EF）有条．

查看试题解析
18.
如图所示，在每个边长都为1的小正方形组成的网格中，点A，B，C均为格点．
（Ⅰ）线段AB的长度等于 $\underline{}$
（Ⅱ）若P为线段AB上的动点，以PC、PA为邻边的四边形PAQC为平行四边形，当PQ长度最小时，请你借助网格和无刻度的直尺画出该平行四边形，并简要说明你的作图方法（不要求证明）．

查看试题解析

三、解答题：

19.
解不等式组 ${\begin{matrix} 3 x - 2 < 2 x ① \\ \frac{1 + x}{2} - 1 \leq x ② \end{matrix}$ 请结合题意填空，完成本题的解答．
（Ⅰ）解不等式①，得
（Ⅱ）解不等式②，得
（Ⅲ）把不等式①和②的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为

查看试题解析
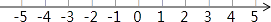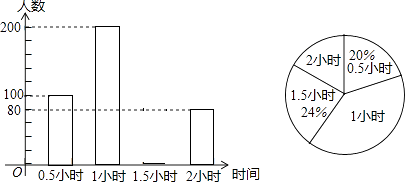
20.
为了解学生参加户外活动的情况，和谐中学对学生每天参加户外活动的时间进行抽样调查，并将调查结果绘制成如图两幅不完整的统计图，根据图示，请回答下列问题：
（Ⅰ）被抽样调查的学生有人，并补全条形统计图；
（Ⅱ）每天户外活动时间的中位数是（小时）；
（Ⅲ）该校共有2000名学生，请估计该校每天户外活动时间超过1小时的学生有人？

查看试题解析
21. 如图，⊙O的直径AB=6，C为圆周上一点，AC=3，过点C作⊙O的切线l，过点B作l的垂线BD，垂足为D，BD与⊙O交于点E．

(1)、求∠AEC的度数；

(2)、求证：四边形OBEC是菱形．

查看试题解析
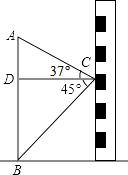
22.
如图，小东在教学楼距地面9米高的窗口C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°，升旗时，国旗上端悬挂在距地面2.25米处，若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
23. 为了提高身体素质，有些人选择到专业的健身中心锻炼身体，某健身中心的消费方式如下：
消费卡
消费方式
普通卡
35元/次
白金卡
280元/张，凭卡免费消费10次再送2次
钻石卡
560元/张，凭卡每次消费不再收费
以上消费卡使用年限均为一年，每位顾客只能购买一张卡，且只限本人使用
（Ⅰ）若每年去该健身中心6次，应选择哪种消费方式更合算？
（Ⅱ）设一年内去该健身中心健身x次（x为正整数），所需总费用为y元，请分别写出选择普通消费和白金卡消费的y与x的函数关系式；
（Ⅲ）若某位顾客每年去该健身中心健身至少18次，请通过计算帮助这位顾客选择最合算的消费方式．

查看试题解析
24.
在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：

第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图①）；

第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图②）．

如图②所示建立平面直角坐标系，请解答以下问题：

（Ⅰ）设直线BM的解析式为y=kx，求k的值；

（Ⅱ）若MN的延长线与矩形ABCD的边BC交于点P，设矩形的边AB=a，BC=b；

（i）若a=2，b=4，求P点的坐标；

（ii）请直接写出a、b应该满足的条件．

查看试题解析
25.
如图，平面直角坐标系中，抛物线y=x²﹣2x与x轴交于O、B两点，顶点为P，连接OP、BP，直线y=x﹣4与y轴交于点C，与x轴交于点D．
（Ⅰ）直接写出点B坐标 $\underline{}$ ；判断△OBP的形状 $\underline{}$ ；
（Ⅱ）将抛物线沿对称轴平移m个单位长度，平移的过程中交y轴于点A，分别连接CP、DP；
（i）若抛物线向下平移m个单位长度，当S_△_PCD= $\sqrt{2}$ S_△_POC时，求平移后的抛物线的顶点坐标；
（ii）在平移过程中，试探究S_△_PCD和S_△_POD之间的数量关系，直接写出它们之间的数量关系及对应的m的取值范围．

查看试题解析

消费卡	消费方式
普通卡	35元/次
白金卡	280元/张，凭卡免费消费10次再送2次
钻石卡	560元/张，凭卡每次消费不再收费