初中数学浙教版九年级下册1.3 解直角三角形（4） 同步训练
试卷更新日期：2019-11-29 类型：同步测试
一、基础夯实
-
1. 如图，一艘船由 港沿北偏东65°方向航行 至 港，然后再沿北偏西40°方向航行至 港， 港在 港北偏东20°方向，则 ， 两港之间的距离为（ ） .
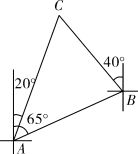A、 B、 C、 D、2. 如图，一艘轮船从位于灯塔C的北偏东60°方向，距离灯塔60 n mile的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东45°方向上的B处，这时轮船B与小岛A的距离是（ ）
A、 n mile B、60 n mile C、120 n mile D、 n mile3. 如图，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东45°方向，然后向西走60米到达C点，测得点B在点C的北偏东60°方向，则这段河的宽度为（ ）
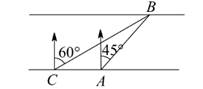A、60（ +1)米 B、30（ +1)米 C、（90-30 )米 D、30（ -1)米4. 如图，甲同学从A地沿北偏西60°方向走100m到B地，再从B地向正南方向走200m到C地，此时甲同学离A地（ ）
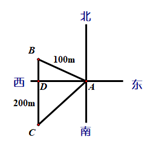A、 m B、100m C、150m D、 m5. 如图，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，此时需把方向调整到与出发一致，则方向的调整应是（ ）
A、右转80° B、左转80° C、右转100° D、左转100°6. 如图，校园内一株树与地面垂直，两次测量它在地面的影长，第一次为太阳光线与地面成60°角时，第二次为太阳光线与地面成30°角时，两次影长差8米，则树高米（结果保留根号）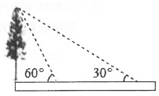
7. 如图，甲、乙两船同时从港口出发，甲船以60海里/时的速度沿北偏东60°方向航行，乙船沿北偏西30°方向航行，半小时后甲船到达C点，乙船正好到达甲船正西方向的B点，则乙船的路程（结果保留根号）
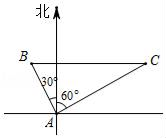8. 如图，某渔船向正东方向以12海里时的速度航行，在A处测得岛C在北偏东的60°方向，1小时后渔船航行到B处，测得岛C在北偏东的30°方向，已知该岛周围10海里内有暗礁．
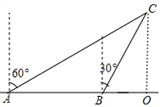(1)、B处离岛C有多远？(2)、如果渔船继续向东航行，需要多长时间到达距离岛C最近的位置？(3)、如果渔船继续向东航行，有无触礁危险？二、提高特训
-
9. 小明从A地向南偏东m°（0＜m＜90）的方向行走到B地，然后向左转30°行走到C地，则下面表述中，正确的个数是（ ）
①B可能在C的北偏西m°方向；②当m＜60时，B在C的北偏西(m＋30)°方向；③B不可能在C的南偏西m°方向；④当m＞60时，B在C的南偏西(150－m)°方向
A、1 B、2 C、3 D、410. 如图，在距离铁轨200米的B处，观察由南宁开往百色的“和谐号”动车，当动车车头在A处时，恰好位于B处的北偏东60°方向上；10秒钟后，动车车头到达C处，恰好位于B处的西北方向上，则这时段动车的平均速度是（ ）米/秒．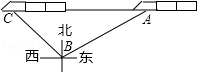
A、20（ +1） B、20（ ﹣1） C、200 D、30011. 如图，已知灯塔M方圆一定范围内有镭射辅助信号，一艘轮船在海上从南向北方向以一定的速度匀速航行，轮船在A处测得灯塔M在北偏东30°方向，行驶1小时后到达B处，此时刚好进入灯塔M的镭射信号区，测得灯塔M在北偏东45°方向，则轮船通过灯塔M的镭射信号区的时间为（ ）
A、（ ﹣1）小时 B、（ +1）小时 C、2小时 D、 小时12. 一艘在南北航线上的测量船，于A点处测得海岛B在点A的南偏东30°方向，继续向南航行30海里到达C点时，测得海岛B在C点的北偏东15°方向，那么海岛B离此航线的最近距离是（ ）（结果保留小数点后两位）（参考数据： ）A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里13. 如图．一艘渔船正以60海里/小时的速度向正东方向航行，在 处测得岛礁 在东北方向上，继续航行1.5小时后到达 处此时测得岛礁 在北偏东 方向，同时测得岛礁 正东方向上的避风港 在北偏东 方向为了在台风到来之前用最短时间到达 处，渔船立刻加速以75海里/小时的速度继续航行小时即可到达 (结果保留根号)
14. 如图，港口A在观测站O的正东方向，OA=40海里，某船从港口A出发，沿北偏东15°方向航行半小时后到达B处，此时从观测站O处测得该船位于北偏东60°的方向．求该船航行的速度 ．
15. 如图为某海域示意图，其中灯塔D的正东方向有一岛屿C.一艘快艇以每小时20nmile的速度向正东方向航行，到达A处时得灯塔D在东北方向上，继续航行0.3h，到达B处时测得灯塔D在北偏东30°方向上，同时测得岛屿C恰好在B处的东北方向上，此时快艇与岛屿C的距离是多少？（结果精确到1nmile.参考数据： ≈1.41， ≈1.73， ≈2.45）
16. 在某校组织的“交通安全宣传教育月”活动中，八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下：在一段笔直的公路上选取两点A、B，在公路另一侧的开阔地带选取一观测点C，在C处测得点A位于C点的南偏西45°方向，且距离为100 米，又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路，限速为60千米/时，兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)、请你帮助他们算一算，这辆小车是否超速？（参考数据： ≈1.41， ≈1.73，计算结果保留两位小数）.(2)、请你以交通警察叔叔的身份对此小轿车的行为作出处理意见，并就乡村公路安全管理提出自己的建议。（处理意见合情合理，建议尽量全面。）17. 如图，海事救援指挥中心A接到海上SOS呼救：一艘渔船B在海上碰到暗礁，船体漏水下沉，5名船员需要援救．经测量渔船B到海岸最近的点C的距离BC=20km，∠BAC=22°37′，指挥中心立即制定三种救援方案（如图1）：①派一艘冲锋舟直接从A开往B；②先用汽车将冲锋舟沿海岸线送到点C，然后再派冲锋舟前往B；③先用汽车将冲锋舟沿海岸线送到距指挥中心33km的点D，然后再派冲锋舟前往B．
已知冲锋舟在海上航行的速度为60km/h，汽车在海岸线上行驶的速度为90km/h．
（sin22°37′= ，cos22°37′= ，tan22°37′= ）
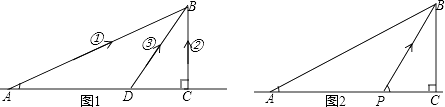(1)、通过计算比较，这三种方案中，哪种方案较好（汽车装卸冲锋舟的时间忽略不计）？(2)、事后，细心的小明发现，上面的三种方案都不是最佳方案，最佳方案应是：先用汽车将冲锋舟沿海岸线送到点P处，点P满足cos∠BPC= （冲锋舟与汽车速度的比），然后再派冲锋舟前往B（如图2）．请你说明理由！如果你反复探索没有解决问题，可以选取①、②、③两种研究方法：
方案①：在线段上AP任取一点M；然后用转化的思想，从几何的角度说明汽车行AM加上冲锋舟行BM的时间比车行AP加上冲锋舟行BP的时间要长．
方案②：在线段上AP任取一点M；设AM=x；然后用含有x的代数式表示出所用时间t；
方案③：利用现有数据，根据cos∠BPC= 计算出汽车行AP加上冲锋舟行BP的时间．