初中数学浙教版九年级下册1.3 解直角三角形（2） 同步训练
试卷更新日期：2019-11-29 类型：同步测试
一、基础夯实
-
1. 如图，某超市自动扶梯的倾斜角 为 ，扶梯长 为 米，则扶梯高 的长为（ ）
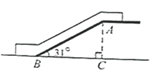A、 米 B、 米 C、 米 D、 米2. 若斜坡的坡比为1： ，则斜坡的坡角等于( )A、30° B、45° C、50° D、60°3. 如图，市政府准备修建一座高AB＝6m的过街天桥，已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为 ，则坡面AC的长度为（ ）m．
A、10 B、8 C、6 D、64. 如图，先锋村准备在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB为（ ）
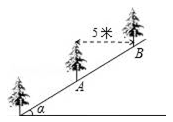A、5cosα B、 C、5sinα D、5. 如图，为了测量山坡护坡石坝的坡度（坡面的铅直高度与水平宽度的比称为坡度），把一根长5m的竹竿AC斜靠在石坝旁，量出杆长1m处的D点离地面的高度DE=0.6m，又量得杆底与坝脚的距离AB=3m，则石坝的坡度为（ ）
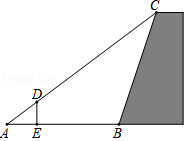A、 B、3 C、 D、46. 如图，河坝横断面迎水坡AB的坡比是 （坡比是坡面的铅直高度BC与水平宽度AC之比），坝高BC=3m，则坡面AB的长度是（ ）
A、9m B、6m C、 m D、 m7. 如图，某单位门前原有四级台阶，每级台阶高为18cm，宽为30cm，为方便残疾人土，拟在门前台阶右侧改成斜坡，设台阶的起点为A点，斜坡的起点为C点，准备设计斜坡BC的坡度i＝1：5，则AC的长度是cm.
8. 如图，一山坡的坡度为i＝1： ，小辰从山脚A出发，沿山坡向上走了200米到达点B，则小辰上升了米．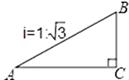
9. 某处欲建一观景平台，如图所示，原设计平台的楼梯长AB=6m，∠ABC=45°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC=30°，则调整后楼梯AD的长为m．（结果保留根号）
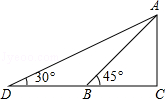10. 自开展“全民健身运动”以来，喜欢户外步行健身的人越来越多，为方便群众步行健身，某地政府决定对一段如图1所示的坡路进行改造．如图2所示，改造前的斜坡 米，坡度为 ；将斜坡 的高度 降低 米后，斜坡 改造为斜坡 ，其坡度为 ．求斜坡 的长．（结果保留根号）
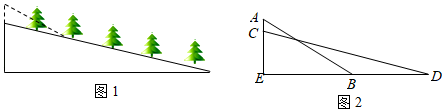11. 某地的一座人行天桥如图所示，天桥高为6米，坡面 的坡度为 ，文化墙 在天桥底部正前方8米处( 的长)，为了方便行人推车过天桥，有关部门决定降低坡度，使新坡面的坡度为 .(参考数据： ， )
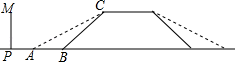(1)、若新坡面坡角为 ，求坡角 度数；(2)、有关部门规定，文化墙距天桥底部小于3米时应拆除，天桥改造后，该文化墙 是否需要拆除？请说明理由.12. Jack同学从点A出发，沿着坡角为α的斜坡向上走了650米到达点B，且sinα= ， 然后又沿着坡比i=1：3的斜坡向上走了500米到达点C。
(1)、Jack从点A到点B上升的高度是多少米？(2)、Jack从点A到点C上升的高度CD是多少米？13. 安装在屋顶的太阳能热水器的横截面示意图如图所示．已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O，⊙O的半径为0.2米，AO与屋面AB的夹角为32°，与铅垂线OD的夹角为40°，BF⊥AB，垂足为B，OD⊥AD，垂足为D，AB＝2米．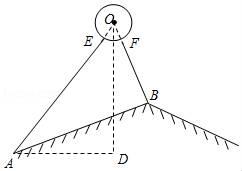
(1)、求支架BF的长；(2)、求屋面AB的坡度．（参考数据：tan18°≈ ，tan32°≈ ，tan40°≈ ）14. 如图，为测量瀑布AB的高度，测量人员在瀑布对面山上的D点处测得瀑布顶端A点的仰角是 ，测得瀑布底端B点的俯角是 ，AB与水平面垂直 又在瀑布下的水平面测得 ， 注：C、G、F三点在同一直线上， 于点 ，斜坡 ，坡角 (参考数据： ， ， ， ， ， ， )
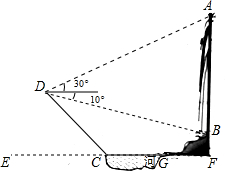(1)、求测量点D距瀑布AB的距离 精确到 ；(2)、求瀑布AB的高度 精确到二、提高特训
-
15. 如图，AB是垂直于水平面的建筑物，为测量AB的高度，小红从建筑底端B点出发，沿水平方向行走了52米到达点C，然后沿斜坡CD前进，到达坡顶D点处，DC=BC，在点D处放置测角仪，测角仪支架DE的高度为0.8米，在E点处测得建筑物顶端A点的仰角∠AEF为27°（点A，B，C，D，E在同一平面内）.斜坡CD的坡度（或坡比）i=1：2.4，那么建筑物AB的高度约为（ ）（参考数据sin27°≈0.45，cos27°≈0.89，tan27°≈0.51）
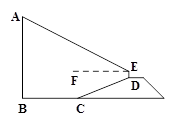A、65.8米 B、71.8米 C、73.8米 D、119.8米.16. 为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动.如图，在一个坡度（或坡比）i＝1：2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC＝26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED＝48°（古树CD与山坡AB的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为（ ）（参考数据：sin48°≈0.73，cos48°≈0.67，tan48°≈1.11）
A、17.0米 B、21.9米 C、23.3米 D、33.3米17. “新中梁山隧道”于2017年11月21日开放通行，原中梁山隧道将封闭升级，扩容改造工程预计2018年3月全部完工，届时将实现双向8车道通行，隧道通行能力将增加一倍，沿线交通拥堵状况将有所缓解．图中线段AB表示该工程的部分隧道．无人勘测机从隧道侧的A点出发时，测得C点正上方的E点的仰角为45°，无人机飞行到E点后，沿着坡度i=1：3的路线EB飞行，飞行到D点正上方的F点时，测得A点的俯角为12°，其中EC=100米，A，B，C，D，E，F在同一平面内，则隧道AD段的长度约为（ ）米，（参考数据：tan12°≈0.2，cosl2°≈0.98）
A、200 B、250 C、300 D、54018. 图中的阴影部分是某水库大坝横截面，小明站在大坝上的A处看到一棵大树CD的影子刚好落在坝底的B处（点A与大树及其影子在同一平面内），此时太阳光与地面的夹角为60°，在A处测得树顶D的俯角为15°，如图所示，已知斜坡AB的坡度i= ：1，若大树CD的高为8 米，则大坝的高为（ ）米（结果精确到1米，参考数据≈1.414 ≈1.732）
A、18 B、19 C、20 D、2119. 如图水库堤坝的横断面是梯形，BC长为30m，CD长为20 m，斜坡AB的坡比为1：3，斜坡CD的坡比为1：2，则坝底的宽AD为m 。
20. 如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图．已知长方体货厢的高度BC为2米，斜坡AB的坡度 ，现把图中的货物沿斜坡继续往前平移，当货物顶点D与C重合时，恰好可把货物放平装进货厢，则BD= ．
21. 某机场为了方便旅客换乘，计划在一、二层之间安装电梯，截面设计图如图所示，已知两层AD与BC平行，层高AB为8米，A、D间水平距离为5米，∠ACB=21.5°
(1)、通过计算说明身高2.4米的人在竖直站立的情况下，搭乘电梯在D处会不会碰到头部；(2)、若采用中段加平台设计（如图虚线所示），已知平台MN∥BC，且AM段和NC段的坡度均为1：2（坡度是指坡面的铅直高度与水平宽度的比），求平台MN的长度．（参考数据：sin21.5°= ，cos21.5°= ，tan21.5°= ）
22. 如图，一座山的一段斜坡BD的长度为600米，且这段斜坡的坡度i=1：3（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角为33°，在斜坡D处测得山顶A的仰角为45°．求山顶A到地面BC的高度AC是多少米？（结果用含非特殊角的三角函数和根式表示即可）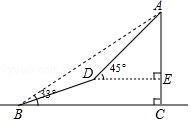
23. 为邓小平诞辰110周年献礼，广安市政府对城市建设进行了整改，如图，已知斜坡AB长60 米，坡角（即∠BAC）为45°，BC⊥AC，现计划在斜坡中点D处挖去部分斜坡，修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE（下面两个小题结果都保留根号）．
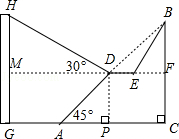(1)、若修建的斜坡BE的坡比为 ：1，求休闲平台DE的长是多少米？(2)、一座建筑物GH距离A点33米远（即AG＝33米），小亮在D点测得建筑物顶部H的仰角（即∠HDM）为30°．点B、C、A、G，H在同一个平面内，点C、A、G在同一条直线上，且HG⊥CG，问建筑物GH高为多少米？