2017年东北三省四市高考数学二模试卷(理科)
试卷更新日期:2017-07-20 类型:高考模拟
一、选择题
-
1. 已知复数z=1+2i,则 =( )A、5 B、5+4i C、﹣3 D、3﹣4i2. 已知集合A={x|x2﹣2x﹣3<0},B={x||x|<2}则A∩B=( )A、{x|﹣2<x<2} B、{x|﹣2<x<3} C、{x|﹣1<x<3} D、{x|﹣1<x<2}3. 祖暅原理:“幂势既同,则积不容异”.它是中国古代一个设计几何体体积的问题.意思是如果两个等高的几何体在同高处处截得两几何体的截面面积恒等,那么这两个几何体的体积相等.设A,B为两个等高的几何体,p:A,B的体积不相等,q:A,B在同高处的截面面积不恒相等,根据祖暅原理可知,p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为( )A、2 B、 C、 D、5. 已知数列{an}满足an+1﹣an=2,a1=﹣5,则|a1|+|a2|+…+|a6|=( )A、9 B、15 C、18 D、306. 平面内的动点(x,y)满足约束条件 ,则z=2x+y的取值范围是( )A、(﹣∞,+∞) B、(﹣∞,4] C、[4,+∞) D、[﹣2,2]7. 某几何体的三视图如图所示,则其体积为( )
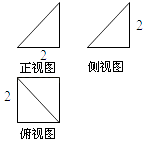 A、4 B、 C、 D、8. 将一枚质地均匀的硬币连续抛掷n次,事件“至少有一次正面向上”的概率为 ,则n的最小值为( )A、4 B、5 C、6 D、79. 若方程 在 上有两个不相等的实数解x1 , x2 , 则x1+x2=( )A、 B、 C、 D、10. 运行如图所示的程序框图,则输出的a、b、c满足( )
A、4 B、 C、 D、8. 将一枚质地均匀的硬币连续抛掷n次,事件“至少有一次正面向上”的概率为 ,则n的最小值为( )A、4 B、5 C、6 D、79. 若方程 在 上有两个不相等的实数解x1 , x2 , 则x1+x2=( )A、 B、 C、 D、10. 运行如图所示的程序框图,则输出的a、b、c满足( ) A、c≤b≤a B、a≤b≤c C、a≤c≤b D、b≤c≤a11. 已知向量 , ,若m+n=1,则 |的最小值为( )A、 B、 C、 D、12. 对函数f(x)= ,若∀a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )A、 B、 C、 D、
A、c≤b≤a B、a≤b≤c C、a≤c≤b D、b≤c≤a11. 已知向量 , ,若m+n=1,则 |的最小值为( )A、 B、 C、 D、12. 对函数f(x)= ,若∀a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 现将5张连号的电影票分给甲乙等5个人,每人一张,且甲乙分得的电影票连号,则共有种不同的分法(用数字作答).14. 函数f(x)=ex•sinx在点(0,f(0))处的切线方程是 .15. 等比数列{an}中各项均为正数,Sn是其前n项和,且满足2S3=8a1+3a2 , a4=16,则S4= .16. F是双曲线 的左焦点,过F作某一渐近线的垂线,分别与两条渐近线相交于A,B两点,若 ,则双曲线的离心率为 .
三、解答题
-
17. 已知点P( ,1),Q(cosx,sinx),O为坐标原点,函数f(x)= • .
(Ⅰ)求函数f(x)的解析式及f(x)的最小正周期;
(Ⅱ)若A为△ABC的内角,f(A)=4,BC=3,求△ABC周长的最大值.
18. 某手机厂商推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
20
40
80
50
10
男性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
频数
45
75
90
60
30
(Ⅰ)完成下列频率分布直方图,并比较女性用户和男性用户评分的波动大小(不计算具体值,给出结论即可);
(Ⅱ)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和期望.
19. 如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点. (1)、求证:PD⊥平面ABE;(2)、若F为AB中点, ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为 .20. 椭圆C: 的长轴长为2 ,P为椭圆C上异于顶点的一个动点,O为坐标原点,A2为椭圆C的右顶点,点M为线段PA2的中点,且直线PA2与直线OM的斜率之积为﹣ .(1)、求椭圆C的方程;(2)、过椭圆C的左焦点F1且不与坐标轴垂直的直线l交椭圆C于两点A,B,线段AB的垂直平分线与x轴交于点N,N点的横坐标的取值范围是 ,求线段AB的长的取值范围.21. 已知函数f(x)=(1)、求函数f(x)的极值;(2)、当0<x<e时,证明:f(e+x)>f(e﹣x);(3)、设函数f(x)的图象与直线y=m的两个交点分别为A(x1 , y1),B(x2 , y2),AB的中点的横坐标为x0 , 证明:f'(x0)<0.
(1)、求证:PD⊥平面ABE;(2)、若F为AB中点, ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为 .20. 椭圆C: 的长轴长为2 ,P为椭圆C上异于顶点的一个动点,O为坐标原点,A2为椭圆C的右顶点,点M为线段PA2的中点,且直线PA2与直线OM的斜率之积为﹣ .(1)、求椭圆C的方程;(2)、过椭圆C的左焦点F1且不与坐标轴垂直的直线l交椭圆C于两点A,B,线段AB的垂直平分线与x轴交于点N,N点的横坐标的取值范围是 ,求线段AB的长的取值范围.21. 已知函数f(x)=(1)、求函数f(x)的极值;(2)、当0<x<e时,证明:f(e+x)>f(e﹣x);(3)、设函数f(x)的图象与直线y=m的两个交点分别为A(x1 , y1),B(x2 , y2),AB的中点的横坐标为x0 , 证明:f'(x0)<0.