初中数学浙教版九年级下册1.1 锐角三角函数-特殊角的三角函数 同步训练
试卷更新日期:2019-11-29 类型:同步测试
一、基础夯实
-
1. tan45°的值为( )A、 B、1 C、 D、2. ﹣sin60°的倒数为( )A、﹣2 B、
 C、﹣
C、﹣ 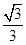 D、﹣
D、﹣ 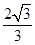 3. 已知锐角A,且sinA= ,则∠A等于( )A、60° B、45° C、30° D、15°4. 在△ABC中,若∠A、∠B满足|cosA﹣ |+(sinB﹣ )2=0,则∠C=( )A、45° B、60° C、75° D、105°5. Rt△ABC中,∠A:∠B:∠C=1:2:3,则sinB=( )A、
3. 已知锐角A,且sinA= ,则∠A等于( )A、60° B、45° C、30° D、15°4. 在△ABC中,若∠A、∠B满足|cosA﹣ |+(sinB﹣ )2=0,则∠C=( )A、45° B、60° C、75° D、105°5. Rt△ABC中,∠A:∠B:∠C=1:2:3,则sinB=( )A、 B、
B、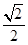 C、
C、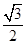 D、1
6. 若锐角三角函数tan55°=a,则a的范围是( )A、0<a<1 B、1<a<2 C、2<a<3 D、3<a<47. 计算:sin30°-3tan60°+cos245°。8. 计算:3tan30°+cos60°- +2sin245°9. 计算: ﹣sin30°(cos45°﹣sin60°)10. 计算:(1)、cos45°+3tan30°﹣2sin60°(2)、2cos30°﹣ .11. 如图,已知△ABC中,∠C=90°,且sinA= ,BC=1.5,求AC.
D、1
6. 若锐角三角函数tan55°=a,则a的范围是( )A、0<a<1 B、1<a<2 C、2<a<3 D、3<a<47. 计算:sin30°-3tan60°+cos245°。8. 计算:3tan30°+cos60°- +2sin245°9. 计算: ﹣sin30°(cos45°﹣sin60°)10. 计算:(1)、cos45°+3tan30°﹣2sin60°(2)、2cos30°﹣ .11. 如图,已知△ABC中,∠C=90°,且sinA= ,BC=1.5,求AC.
二、提高特训
-
12. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或1713. 已知α为锐角,sin(α+20°)= ,则α的度数为( )A、20° B、40° C、60° D、80°14. △ABC中,∠A,∠B均为锐角,且(tanB﹣ )(2sinA﹣ )=0,则△ABC一定是( )
A、等腰三角形 B、等边三角形 C、直角三角形 D、有一个角是60°的三角形15. 关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ
cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ
tan(α+β)= (1﹣tanαtanβ≠0),
合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°= =1。
利用上述公式计算下列三角函数①sin105°= ,②tan105°=﹣2﹣ ,③sin15°= ,④cos90°=0.
其中正确的个数有( )
A、1个 B、2个 C、3个 D、4个