2017年湖北省黄石市中考数学试卷
试卷更新日期:2017-07-20 类型:中考真卷
一、选择题
-
1. 下列各数是有理数的是( )A、﹣ B、 C、 D、π
-
2. 地球绕太阳公转的速度约为110000km/h,则110000用科学记数法可表示为( )A、0.11×106 B、1.1×105 C、0.11×105 D、1.1×106
-
3. 下列图形中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4. 下列运算正确的是( )A、a0=0 B、a2+a3=a5 C、a2•a﹣1=a D、+ =
-
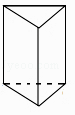
5. 如图,该几何体主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
6. 下表是某位男子马拉松长跑运动员近6次的比赛成绩(单位:分钟)
第几次
1
2
3
4
5
6
比赛成绩
145
147
140
129
136
125
则这组成绩的中位数和平均数分别为( )
A、137、138 B、138、137 C、138、138 D、137、139 -
7. 如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE= ,则∠CDE+∠ACD=( )
 A、60° B、75° C、90° D、105°
A、60° B、75° C、90° D、105° -
8. 如图,是二次函数y=ax2+bx+c的图象,对下列结论①ab>0,②abc>0,③ <1,其中错误的个数是( )
 A、3 B、2 C、1 D、0
A、3 B、2 C、1 D、0 -
9. 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
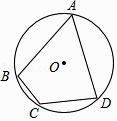 A、 B、 C、 D、
A、 B、 C、 D、 -
10. 如图,已知凸五边形ABCDE的边长均相等,且∠DBE=∠ABE+∠CBD,AC=1,则BD必定满足( )
 A、BD<2 B、BD=2 C、BD>2 D、以上情况均有可能
A、BD<2 B、BD=2 C、BD>2 D、以上情况均有可能
二、填空题
-
11. 因式分解:x2y﹣4y= .
-
12. 分式方程 = ﹣2的解为 .
-
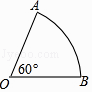
13. 如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为 .
-
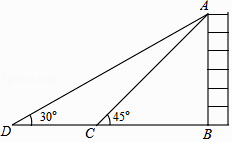
14. 如图所示,为了测量出一垂直水平地面的某高大建筑物AB的高度,一测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角大小为30°,则建筑物AB的高度约为米.
(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据: ≈1.41, ≈1.73)
-
15. 甲、乙两位同学各抛掷一枚质地均匀的骰子,他们抛掷的点数分别记为a、b,则a+b=9的概率为 .
-
16. 观察下列格式:
=1﹣ =
+ =1﹣ + ﹣ =
+ + =1﹣ + ﹣ + ﹣ =
…
请按上述规律,写出第n个式子的计算结果(n为正整数) . (写出最简计算结果即可)
三、解答题
-
17. 计算:(﹣2)3+ +10+|﹣3+ |.
-
18. 先化简,再求值:( ﹣ )÷ ,其中a=2sin60°﹣tan45°.
-
19. 已知关于x的不等式组 恰好有两个整数解,求实数a的取值范围.
-
20. 已知关于x的一元二次方程x2﹣4x﹣m2=0(1)、求证:该方程有两个不等的实根;(2)、若该方程的两个实数根x1、x2满足x1+2x2=9,求m的值.
-
21. 如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
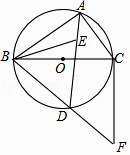 (1)、求证:DB=DE;(2)、求证:直线CF为⊙O的切线
(1)、求证:DB=DE;(2)、求证:直线CF为⊙O的切线 -
22. 随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗1L的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示:

(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)、试求进行该试验的车辆数;(2)、请补全频数分布直方图;(3)、若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油1L的情况下可以行驶13km以上? -
23. 小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律:
①该蔬菜的销售价P(单位:元/千克)与时间x(单位:月份)满足关系:P=9﹣x
②该蔬菜的平均成本y(单位:元/千克)与时间x(单位:月份)满足二次函数关系y=ax2+bx+10,已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)、求该二次函数的解析式;(2)、请运用小明统计的结论,求出该蔬菜在第几月份的平均利润L(单位:元/千克)最大?最大平均利润是多少?(注:平均利润=销售价﹣平均成本) -
24. 在现实生活中,我们会看到许多“标准”的矩形,如我们的课本封面、A4的打印纸等,其实这些矩形的长与宽之比都为 :1,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形”ABCD中,P为DC边上一定点,且CP=BC,如图所示.(1)、
如图①,求证:BA=BP;
 (2)、
(2)、如图②,点Q在DC上,且DQ=CP,若G为BC边上一动点,当△AGQ的周长最小时,求 的值;
 (3)、
(3)、如图③,已知AD=1,在(2)的条件下,连接AG并延长交DC的延长线于点F,连接BF,T为BF的中点,M、N分别为线段PF与AB上的动点,且始终保持PM=BN,请证明:△MNT的面积S为定值,并求出这个定值.

-
25. 如图,直线l:y=kx+b(k<0)与函数y= (x>0)的图象相交于A、C两点,与x轴相交于T点,过A、C两点作x轴的垂线,垂足分别为B、D,过A、C两点作y轴的垂线,垂足分别为E、F;直线AE与CD相交于点P,连接DE,设A、C两点的坐标分别为(a, )、(c, ),其中a>c>0.(1)、
如图①,求证:∠EDP=∠ACP;
 (2)、
(2)、如图②,若A、D、E、C四点在同一圆上,求k的值;
 (3)、
(3)、如图③,已知c=1,且点P在直线BF上,试问:在线段AT上是否存在点M,使得OM⊥AM?请求出点M的坐标;若不存在,请说明理由.

