初中数学浙教版九年级下册1.1 锐角三角函数-定义 同步训练
试卷更新日期：2019-11-29 类型：同步测试
一、基础夯实
-
1. 在Rt△ABC中，∠C=90°，则 是∠A的（ ）A、正弦 B、余弦 C、正切 D、以上都不对2. 在Rt△ABC中，∠C＝90°，如果∠A＝α，AB＝3，那么AC等于（ ）A、3sinα B、3cosα C、 D、3. 如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（ ）
A、
B、
C、
D、2
4. 正方形网格中，∠AOB如图放置，则tan∠AOB的值为（ ）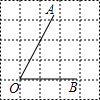
A、2 B、
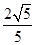C、
D、
5. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA=（ ）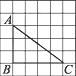
A、 B、 C、 D、6. 如图，某游乐场一山顶滑梯的高为h，滑梯的坡角为α，那么滑梯长l为（ ）
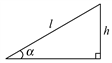A、 B、 C、 D、h·sinα7. 如图，自动扶梯AB段长为20米，倾斜角为a，高度BC为（ ）米
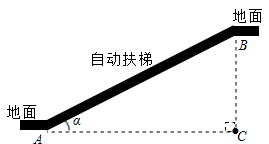A、 B、20cosa C、20sina D、20tana8. 如图，某学校数学课外活动小组的同学们，为了测量一个小湖泊两岸的两棵树A和B之间的距离，在垂直AB的方向AC上确定点C，如果测得AC＝75米，∠ACB＝55°，那么A和B之间的距离是（ ）米．
A、75•sin55° B、75•cos55° C、75•tan55° D、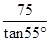
9. 已知Rt△ABC中，∠C=90°，AC=3，∠B=37°，则BC的长为（注：tan∠B=0.75，sin∠B=0.6，cos∠B=0.8）
10. 在△ABC中，∠C＝90°，AB＝13，BC＝5，求∠A的正弦值、余弦值和正切值．二、提高特训
-
11. 把△ABC的各边长都增加两倍，则锐角A的正弦值（ ）A、增加2倍 B、增加4倍 C、不变 D、不能确定12. 如图，P是∠α的边OA上一点，且点P的横坐标为3，sinα＝ ，则tanα＝（ ）
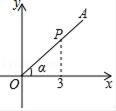A、 B、 C、 D、13. 在Rt△ACB中，∠C=90°，BC=6，cosA= ，则AC的长为（ ）A、4.8 B、7.5 C、8 D、1014. 如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝ ，AB的垂直平分线ED交BC的延长线于D点，垂足为E ， 则sin∠CAD＝（ ）
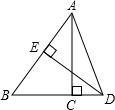A、 B、 C、 D、15. 已知tanα= ，那么sinα= ． （其中α为锐角）16. 如图，在Rt△ABC中，∠C＝90°，AB＝4，BC＝1，则cosA的值是 ．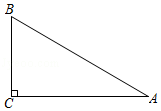
，