2017年广西玉林市、崇左市中考数学试卷

试卷更新日期：2017-07-20 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列四个数中最大的数是（）

A、0 B、﹣1 C、﹣2 D、﹣3

查看试题解析
2. 如图，直线a，b被c所截，则∠1与∠2是（）

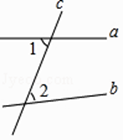A、同位角 B、内错角 C、同旁内角 D、邻补角

查看试题解析
3. 一天时间为86400秒，用科学记数法表示这一数字是（）

A、864×10² B、86.4×10³ C、8.64×10⁴ D、0.864×10⁵

查看试题解析
4. 一组数据：6，3，4，5，7的平均数和中位数分别是（）

A、5，5 B、5，6 C、6，5 D、6，6

查看试题解析
5. 下列运算正确的是（）

A、（a³）²=a⁵ B、a²•a³=a⁵ C、a⁶÷a²=a³ D、3a²﹣2a²=1

查看试题解析
6. 如图所示的几何体的俯视图是（）

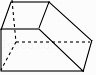A、 B、 C、 D、

查看试题解析
7.
五星红旗上的每一个五角星（）

A、是轴对称图形，但不是中心对称图形 B、是中心对称图形，但不是轴对称图形 C、既是轴对称图形，又是中心对称图形 D、既不是轴对称图形，也不是中心对称图形

查看试题解析
8. 对于函数y=﹣2（x﹣m）²的图象，下列说法不正确的是（）

A、开口向下 B、对称轴是x=m C、最大值为0 D、与y轴不相交

查看试题解析
9. 如图，在矩形ABCD中，AB＞BC，点E，F，G，H分别是边DA，AB，BC，CD的中点，连接EG，HF，则图中矩形的个数共有（）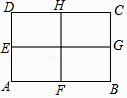

A、5个 B、8个 C、9个 D、11个

查看试题解析
10.
如图，一艘轮船在A处测得灯塔P位于其北偏东60°方向上，轮船沿正东方向航行30海里到达B处后，此时测得灯塔P位于其北偏东30°方向上，此时轮船与灯塔P的距离是（）

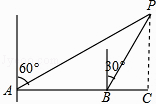A、15 $\sqrt{3}$ 海里 B、30海里 C、45海里 D、30 $\sqrt{3}$ 海里

查看试题解析
11. 如图，大小不同的两个磁块，其截面都是等边三角形，小三角形边长是大三角形边长的一半，点O是小三角形的内心，现将小三角形沿着大三角形的边缘顺时针滚动，当由①位置滚动到④位置时，线段OA绕点O顺时针转过的角度是（）

A、240° B、360° C、480° D、540°

查看试题解析
12. 如图，AB是⊙O的直径，AC，BC分别与⊙O相交于点D，E，连接DE，现给出两个命题：
①若AC=AB，则DE=CE；
②若∠C=45°，记△CDE的面积为S₁ ，四边形DABE的面积为S₂ ，则S₁=S₂ ，
那么（）

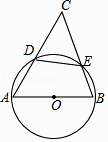A、①是真命题②是假命题 B、①是假命题②是真命题 C、①是假命题②是假命题 D、①是真命题②是真命题

查看试题解析

二、填空题

13. |﹣1|= ．

查看试题解析
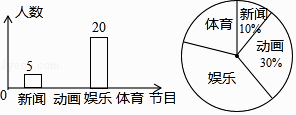
14. 若4a²b²ⁿ⁺¹与a^mb³是同类项，则m+n= ．

查看试题解析
15. 分解因式：a³﹣ab²= ．

查看试题解析
16. 如图是小强根据全班同学喜爱四类电视节目的人数而绘制的两幅不完整的统计图，则喜爱“体育”节目的人数是人．

查看试题解析
17. 如图，在边长为2的正八边形中，把其不相邻的四条边均向两边延长相交成一个四边形ABCD，则四边形ABCD的周长是．

查看试题解析
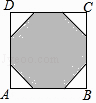18. 已知抛物线：y=ax²+bx+c（a＞0）经过A（﹣1，1），B（2，4）两点，顶点坐标为（m，n），有下列结论：
①b＜1；②c＜2；③0＜m＜ $\frac{1}{2}$ ；④n≤1．
则所有正确结论的序号是．

查看试题解析

三、解答题

19. 计算：（2017﹣π）⁰+ $\sqrt[3]{8}$ ﹣2tan45°．

查看试题解析
20. 化简：（a+1﹣ $\frac{3}{a - 1}$ ）÷ $\frac{a - 2}{2 a - 2}$ ，然后给a从1，2，3中选取一个合适的数代入求值．

查看试题解析
21. 已知关于x的一元二次方程：x²﹣（t﹣1）x+t﹣2=0．

(1)、求证：对于任意实数t，方程都有实数根；

(2)、当t为何值时，方程的两个根互为相反数？请说明理由．

查看试题解析
22. 在一个不透明的袋子中有一个黑球a和两个白球b，c（除颜色外其他均相同）．用树状图（或列表法）解答下列问题：

(1)、小丽第一次从袋子中摸出一个球不放回，第二次又从袋子中摸出一个球．则小丽两次都摸到白球的概率是多少？

(2)、小强第一次从袋子中摸出一个球，摸到黑球不放回，摸到白球放回；第二次又从袋子中摸出一个球，则小强两次都摸到白球的概率是多少？

查看试题解析
23. 如图，AB是⊙O的直径，AC是上半圆的弦，过点C作⊙O的切线DE交AB的延长线于点E，过点A作切线DE的垂线，垂足为D，且与⊙O交于点F，设∠DAC，∠CEA的度数分别是α，β．

(1)、用含α的代数式表示β，并直接写出α的取值范围；

(2)、连接OF与AC交于点O′，当点O′是AC的中点时，求α，β的值．

查看试题解析
24. 某新建成学校举行美化绿化校园活动，九年级计划购买A，B两种花木共100棵绿化操场，其中A花木每棵50元，B花木每棵100元．

(1)、若购进A，B两种花木刚好用去8000元，则购买了A，B两种花木各多少棵？

(2)、如果购买B花木的数量不少于A花木的数量，请设计一种购买方案使所需总费用最低，并求出该购买方案所需总费用．

查看试题解析
25. 如图，在等腰直角三角形ABC中，∠ACB=90°，AC=BC=4，D是AB的中点，E，F分别是AC，BC上的点（点E不与端点A，C重合），且AE=CF，连接EF并取EF的中点O，连接DO并延长至点G，使GO=OD，连接DE，DF，GE，GF．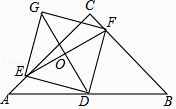

(1)、求证：四边形EDFG是正方形；

(2)、当点E在什么位置时，四边形EDFG的面积最小？并求四边形EDFG面积的最小值．

查看试题解析
26.
如图，一次函数y=k₁x+5（k₁＜0）的图象与坐标轴交于A，B两点，与反比例函数y= $\frac{k_{2}}{x}$ （k₂＞0）的图象交于M，N两点，过点M作MC⊥y轴于点C，已知CM=1．

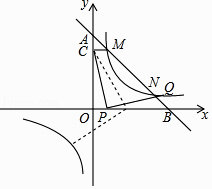(1)、求k₂﹣k₁的值；

(2)、若 $\frac{A M}{A N}$ = $\frac{1}{4}$ ，求反比例函数的解析式；

(3)、在（2）的条件下，设点P是x轴（除原点O外）上一点，将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ，当点P滑动时，点Q能否在反比例函数的图象上？如果能，求出所有的点Q的坐标；如果不能，请说明理由．

查看试题解析