2017年四川省绵阳市三台县中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列运算中，正确的是（）

A、 $\sqrt{9} = \pm 3$ B、（a²）³=a⁶ C、3a•2a=6a D、3^﹣²=﹣6

查看试题解析
2. H7N9时一种新型禽流感，其病毒颗粒呈多形性，其中球形病毒的最大直径为0.00000012米，这一直径用科学记数法表示为（）

A、1.2×10^﹣⁷米 B、1.2×10^﹣⁸米 C、12×10^﹣⁸米 D、12×10^﹣⁹米

查看试题解析
3. 如图，几何体的三视图对应的正三棱柱是（）

A、 B、 C、 D、

查看试题解析
4. 关于x的不等式组 ${\begin{matrix} x > a \\ x > 1 \end{matrix}$ 的解集为x＞1，则a的取值范围是（）

A、a＞1 B、a＜1 C、a≥1 D、a≤1

查看试题解析
5. 下列关于矩形的说法，正确的是（）

A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线相等且互相平分 D、矩形的对角线互相垂直且平分

查看试题解析
6. 已知A（x₁ ， y₁），B（x₂ ， y₂）是反比例函数y=﹣ $\frac{k^{2}}{x}$ 图象上的两个点，且x₁＜x₂ ，则y₁与y₂的大小关系是（）

A、y₁＜y₂ B、y₁=y₂ C、y₁＞y₂ D、大小不确定

查看试题解析
7. “关于x的函数y=（1﹣m）x²+2x+1的图象与x轴至少有一个交点”是真命题，则m的值不可以是（）

A、m=1 B、m=0 C、m=﹣1 D、m=2

查看试题解析
8. 如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（）

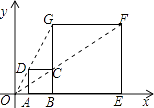A、（3，2） B、（3，1） C、（2，2） D、（4，2）

查看试题解析
9. 如图，已知AD是等腰△ABC底边BC上的高，sinB= $\frac{4}{5}$ ，点E在AC上，且AE：EC=2：3，则tan∠ADE=（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{2}{5}$

查看试题解析
10. 如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{8 \sqrt{13}}{13}$ D、 $\frac{12 \sqrt{13}}{13}$

查看试题解析
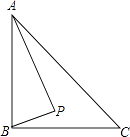11.
如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（）
①AE=BF；②AE⊥BF；③sin∠BQP= $\frac{4}{5}$ ；④S_四边形_ECFG=2S_△_BGE ．

A、4 B、3 C、2 D、1

查看试题解析

二、填空题：

12. 若等式x²+px+q=（x+1）（x﹣3）成立，则p+q= ．

查看试题解析
13. 如图，四边形ABCD中，AB∥CD，AD=CD，E、F分别是AB、BC的中点，若∠1=30°，则∠DAC= ．

查看试题解析
14. 已知x= $\frac{\sqrt{5} - 1}{2}$ ，y= $\frac{\sqrt{5} + 1}{2}$ ，则x²+y²﹣xy的值是．

查看试题解析
15. 平面直角坐标系xOy中有四点A（﹣2，0），B（﹣1，0），C（0，1），D（0，2）在A、B、C、D中取两点与点O为顶点作三角形，所作三角形是等腰直角三角形的概率是．

查看试题解析
16. 如图，半径为5的半圆的初始状态是直径平行于桌面上的直线b，然后把半圆沿直线b进行无滑动滚动，使半圆的直径与直线b重合为止，则圆心O运动路径的长度等于．

查看试题解析
17. 等腰△ABC中，当顶角A的大小确定时，它的对边BC与邻边（腰AB或AC）的比值确定，记为f（A），易得f（60°）=1．若α是等腰三角形的顶角，则f（α）的取值范围是．

查看试题解析

三、解答题

18. 计算：（﹣1）²⁰¹⁷+3（tan60°）^﹣¹﹣|1﹣ $\sqrt{3}$ |+（3.14﹣π）⁰ ．

查看试题解析
19. 解方程： $\frac{3 - x}{x - 4}$ ﹣x= $\frac{1}{4 - x}$ ．

查看试题解析
20. “校园安全”受到全社会的广泛关注，绵阳市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了如图两幅尚不完整的统计图，请你根据统计图中所提供的信息解答下列问题：

(1)、接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为；

(2)、请补全条形统计图；

(3)、若该中学共有学生3000人，请根据上述调查结果，估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数；

(4)、若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．

查看试题解析
21. 已知一次函数y₁=x+m的图象与反比例函数y₂= $\frac{6}{x}$ 的图象交于A、B两点，已知当x＞1时，y₁＞y₂；当0＜x＜1时，y₁＜y₂ ．

(1)、求一次函数的函数表达式；

(2)、已知反比例函数在第一象限的图象上有一点C到x轴的距离为2，求△ABC的面积．

查看试题解析
22. 如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC与⊙O的交点，连接AF．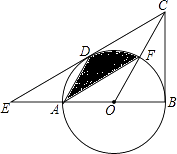

(1)、求证：CB是⊙O的切线；

(2)、若∠ECB=60°，AB=6，求图中阴影部分的面积．

查看试题解析
23. 某家电销售商场电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商场用80000元购进电冰箱的数量与用64000元购进空调的数量相等．

(1)、求每台电冰箱与空调的进价分别是多少？

(2)、现在商场准备一次购进这两种家电共100台，设购进电冰箱x台，这100台家电的销售总利润为y元，要求购进空调数量不超过电冰箱数量的2倍，总利润不低于13200元，请分析合理的方案共有多少种？并确定获利最大的方案以及最大利润．

查看试题解析
24.
如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，连接AF．取AF中点M，EF的中点N，连接MD、MN．

(1)、尝试探究：
结论1：DM、MN的数量关系是；
结论2：DM、MN的位置关系是；

(2)、猜想论证：证明你的结论．

(3)、
拓展：如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，（1）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．

查看试题解析
25.
如图，抛物线y=﹣x²+bx+c（a≠0）与x轴、y轴分别交于点A（3，0）、B（0，3）两点．

(1)、试求抛物线的解析式和直线AB的解析式；

(2)、动点E从O点沿OA方向以1个单位/秒的速度向终点A匀速运动，同时动点F沿AB方向以 $\sqrt{2}$ 个单位/秒的速度向终点B匀速运动，E、F任意一点到达终点时另一个点停止运动，连接EF，设运动时间为t，当t为何值时△AEF为直角三角形？

(3)、抛物线位于第一象限的图象上是否存在一点P，使△PAB面积最大？如果存在，请求出点P的坐标；如果不存在，请说明理由．

查看试题解析