2017年上海市浦东新区中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题:
-
1. 下列实数中,是无理数的为( )A、3.14 B、 C、 D、2. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、3. 函数y=kx﹣1(常数k>0)的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 某幢楼10户家庭每月的用电量如下表所示:
用电量(度)
140
160
180
200
户数
1
3
4
2
那么这10户家庭该月用电量的众数和中位数分别是( )
A、180,180 B、180,160 C、160,180 D、160,1605. 已知两圆的半径分别为1和5,圆心距为4,那么两圆的位置关系是( )A、外离 B、外切 C、相交 D、内切6. 如图,已知△ABC和△DEF,点E在BC边上,点A在DE边上,边EF和边AC相交于点G.如果AE=EC,∠AEG=∠B,那么添加下列一个条件后,仍无法判定△DEF与△ABC一定相似的是( )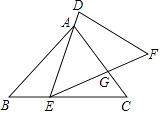 A、 = B、 = C、 = D、 =
A、 = B、 = C、 = D、 =二、填空题:
-
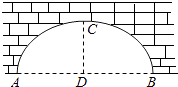
7. 计算:a•a2= .8. 因式分解:x2﹣2x= .9. 方程 =﹣x的根是 .10. 函数f(x)= 的定义域是 .11. 如果方程x2﹣2x+m=0有两个实数根,那么m的取值范围是 .12. 计算:2 + ( + ) .13. 将抛物线y=x2+2x﹣1向上平移4个单位后,所得新抛物线的顶点坐标是 .14. 一个不透明的袋子里装有3个白球、1个红球,这些球除了颜色外无其他的差异,从袋子中随机摸出1个球,恰好是白球的概率是 .15. 正五边形的中心角的度数是 .16. 如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,那么圆弧形桥拱所在圆的半径是米.
 17. 如果一个三角形一边上的中线的长与另两边中点的连线段的长相等,我们称这个三角形为“等线三角形”,这条边称为“等线边”.在等线三角形ABC中,AB为等线边,且AB=3,AC=2,那么BC= .18. 如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= .
17. 如果一个三角形一边上的中线的长与另两边中点的连线段的长相等,我们称这个三角形为“等线三角形”,这条边称为“等线边”.在等线三角形ABC中,AB为等线边,且AB=3,AC=2,那么BC= .18. 如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= .
三、解答题:
-
19. 计算:|2﹣ |﹣8 +2﹣2+ .20. 解不等式组: .21. 已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2 ,sin∠AOC= ,反比例函数y= 的图象经过点C以及边AB的中点D.
 (1)、求这个反比例函数的解析式;(2)、四边形OABC的面积.22. 某文具店有一种练习簿出售,每本的成本价为2元,在销售的过程中价格有些调整,按原来的价格每本8.25元,卖出36本;经过两次涨价,按第二次涨价后的价格卖出了25本.发现按原价格和第二次涨价后的价格销售,分别获得的销售利润恰好相等.(1)、求第二次涨价后每本练习簿的价格;(2)、在两次涨价过程中,假设每本练习簿平均获得利润的增长率完全相同,求这个增长率.
(1)、求这个反比例函数的解析式;(2)、四边形OABC的面积.22. 某文具店有一种练习簿出售,每本的成本价为2元,在销售的过程中价格有些调整,按原来的价格每本8.25元,卖出36本;经过两次涨价,按第二次涨价后的价格卖出了25本.发现按原价格和第二次涨价后的价格销售,分别获得的销售利润恰好相等.(1)、求第二次涨价后每本练习簿的价格;(2)、在两次涨价过程中,假设每本练习簿平均获得利润的增长率完全相同,求这个增长率.(注:利润增长率= ×100%)
23. 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=CD,点E、F分别在边BC、CD上,且BE=DF=AD,联结DE,联结AF、BF分别与DE交于点G、P. (1)、求证:AB=BF;(2)、如果BE=2EC,求证:DG=GE.24. 已知:抛物线y=ax2+bx﹣3经过点A(7,﹣3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D.
(1)、求证:AB=BF;(2)、如果BE=2EC,求证:DG=GE.24. 已知:抛物线y=ax2+bx﹣3经过点A(7,﹣3),与x轴正半轴交于点B(m,0)、C(6m、0)两点,与y轴交于点D. (1)、求m的值;(2)、求这条抛物线的表达式;(3)、点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.25. 如图所示,∠MON=45°,点P是∠MON内一点,过点P作PA⊥OM于点A、PB⊥ON于点B,且PB=2 .取OP的中点C,联结AC并延长,交OB于点D.
(1)、求m的值;(2)、求这条抛物线的表达式;(3)、点P在抛物线上,点Q在x轴上,当∠PQD=90°且PQ=2DQ时,求点P、Q的坐标.25. 如图所示,∠MON=45°,点P是∠MON内一点,过点P作PA⊥OM于点A、PB⊥ON于点B,且PB=2 .取OP的中点C,联结AC并延长,交OB于点D. (1)、求证:∠ADB=∠OPB;(2)、设PA=x,OD=y,求y关于x的函数解析式;(3)、分别联结AB、BC,当△ABD与△CPB相似时,求PA的长.
(1)、求证:∠ADB=∠OPB;(2)、设PA=x,OD=y,求y关于x的函数解析式;(3)、分别联结AB、BC,当△ABD与△CPB相似时,求PA的长.