2017年山东省潍坊市潍城区中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各数中，与﹣2互为相反数的是（）

A、 $\sqrt{{(- 2)}^{2}}$ B、 $\sqrt[3]{- 8}$ C、﹣ $\frac{1}{2}$ D、 $\sqrt{2}$

查看试题解析
2. 下列各组数中，结果相等的是（）

A、﹣1²与（﹣1）² B、 $\frac{2^{3}}{3} 与 {(\frac{2}{3})}^{3}$ C、﹣|﹣2|与﹣（﹣2） D、（﹣3）³与﹣3³

查看试题解析
3. 如图，该几何体的左视图是（）

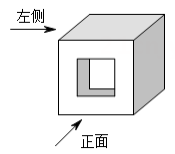A、 B、 C、 D、

查看试题解析
4. 下列运算中，计算正确的是（）

A、2a•3a=6a B、（3a²）³=27a⁶ C、a⁴÷a²=2a D、（a+b）²=a²+ab+b²

查看试题解析
5. 如图，已知AB是⊙O的直径，∠D=36°，则∠CAB的度数为（）

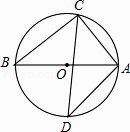A、18° B、36° C、54° D、72°

查看试题解析
6. 若一个圆锥的侧面展开图是一个半径为10cm，圆心角为252°的扇形，则该圆锥的底面半径为（　　）

A、6cm B、7cm C、8cm D、10cm

查看试题解析
7. 如图，在平面直角坐标系中，点P（ $- \frac{1}{2}$ ，a）在直线y=2x+2与直线y=2x+4之间，则a的取值范围是（）

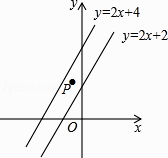A、2＜a＜4 B、1＜a＜3 C、1＜a＜2 D、0＜a＜2

查看试题解析
8. 已知a，b是关于x的一元二次方程x²+nx﹣1=0的两实数根，则式子 $\frac{b}{a} + \frac{a}{b}$ 的值是（）

A、n²+2 B、﹣n²+2 C、n²﹣2 D、﹣n²﹣2

查看试题解析
9. 若方程组 ${\begin{cases} 3 x + y = k + 1 \\ x + 3 y = 3 \end{cases}$ 的解x，y满足0＜x+y＜1，则k的取值范围是（）

A、﹣4＜k＜0 B、﹣1＜k＜0 C、0＜k＜8 D、k＞﹣4

查看试题解析
10. 如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）

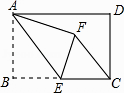A、 $\frac{9}{5}$ B、 $\frac{12}{5}$ C、 $\frac{16}{5}$ D、 $\frac{18}{5}$

查看试题解析
11. 对于二次函数y=﹣x²+2x．有下列四个结论：①它的对称轴是直线x=1；②设y₁=﹣x₁²+2x₁ ， y₂=﹣x₂²+2x₂ ，则当x₂＞x₁时，有y₂＞y₁；③它的图象与x轴的两个交点是（0，0）和（2，0）；④当0＜x＜2时，y＞0．其中正确的结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

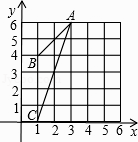
12. 图中△ABC外接圆的圆心坐标是．

查看试题解析
13. 分解因式：（a+5）（a﹣5）+7（a+1）= ．

查看试题解析
14. 若关于x的方程 $\frac{2}{x - 2}$ + $\frac{x + m}{2 - x}$ =2有增根，则m的值是．

查看试题解析
15. 如图，在△ABC中，AB=4，将△ABC绕点B按逆时针方向旋转30°后得到△A₁BC₁ ，则阴影部分的面积为

查看试题解析
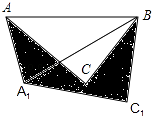16. 如图所示，一次函数y₁=ax+b的图象与反比例函数y₂= $\frac{3}{x}$ 的图象相交于A，B两点，当y₁＞y₂时，﹣1＜x＜0或x＞3，则一次函数的解析式为．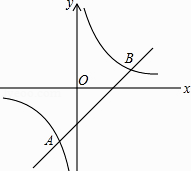

查看试题解析

三、解答题

17. 潍坊到济南的距离约为210km，小刘开着小轿车，小张开着大货车，都从潍坊去济南，小刘比小张晚出发1小时，最后两车同时到达济南，已知小轿车的速度是大货车速度的1.5倍．

(1)、求小轿车和大货车的速度各是多少？（列方程解答）

(2)、当小刘出发时，求小张离济南还有多远？

查看试题解析
18. 今年是第39个植树节，我们提出了“追求绿色时尚，走向绿色文明”的倡议．某校为积极响应这一倡议，立即在八、九年级开展征文活动，校团委对这两个年级各班内的投稿情况进行统计，并制成了如图所示的两幅不完整的统计图．

(1)、求扇形统计图中投稿3篇的班级个数所对应的扇形的圆心角的度数．

(2)、求该校八、九年级各班在这一周内投稿的平均篇数，并将该条形统计图补充完整．

(3)、在投稿篇数最多的4个班中，八、九年级各有两个班，校团委准备从这四个班中选出两个班参加全校的表彰会，请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率．

查看试题解析
19. 如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足 $\frac{C F}{D F} = \frac{1}{3}$ ，连接AF并延长交⊙O于点E，连接AD、DE，若CF=3，AF=4．

(1)、求证：△ADF∽△AED；

(2)、求FG的长；

(3)、求tan∠E的值．

查看试题解析
20.
如图所示，山坡上有一棵与水平面垂直的大树，一场台风过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面．已知山坡的坡角∠AEF=23°，量得树干倾斜角∠BAC=38°，大树被折断部分和坡面所成的角∠ADC=60°，AD=6m．

(1)、求∠CAE的度数；

(2)、求这棵大树折断前的高度？
（结果精确到个位，参考数据： $\sqrt{2}$ =1.4， $\sqrt{3}$ =1.7， $\sqrt{6}$ =2.4）．

查看试题解析
21. 如图甲，在△ABC中，AB=AC，∠BAC=90°．点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．
解答下列问题：

(1)、当点D在线段BC上时（与点B不重合），如图甲，线段CF、BD之间的位置关系为，数量关系为．

(2)、当点D在线段BC的延长线上时，如图乙，①中的结论是否仍然成立，为什么？

查看试题解析
22. 某电子厂生产一种新型电子产品，每件制造成本为20元，试销过程中发现，每月销售量y（万件）与销售单价x（元）之间的关系可以近似地看作一次函数y=﹣2x+100．（利润=售价﹣制造成本）

(1)、写出每月的利润z（万元）与销售单价x（元）之间的函数关系式；

(2)、当销售单价为多少元时，厂商每月获得的利润为400万元？

(3)、根据相关部门规定，这种电子产品的销售单价不能高于40元，如果厂商每月的制造成本不超过520万元，那么当销售单价为多少元时，厂商每月获得的利润最大？最大利润为多少万元？

查看试题解析
23.
如图，在直角坐标系中，以点A（1，0）为圆心，以2为半径的圆与x轴交于B，C两点，与y轴交于D，E两点．

(1)、直接写出B，C，D点的坐标；

(2)、若B、C、D三点在抛物线y=ax²+bx+c上，求出这个抛物线的解析式及它的顶点坐标．

(3)、若圆A的切线交x轴正半轴于点M，交y轴负半轴于点N，切点为P，∠OMN=30°，试判断直线MN是否经过B、C、D三点所在抛物线的顶点？说明理由．

查看试题解析