2017年山东省潍坊市昌乐县中考数学模拟试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 计算﹣12的相反数是( )A、2 B、﹣2 C、1 D、﹣12. 国家文物局2012年6月5日在北京居庸关长城宣布:中国历代长城总长度为21196.18千米.这是中国首次科学、系统地测量历代长城的总长度.数21196.18保留3个有效数字,用科学记数法表示正确的是( )A、2.11×104 B、2.12×104 C、0.212×105 D、0.21×1053. 下列水平放置的几何体中,俯视图是三角形的是( )A、
 圆柱
B、
圆柱
B、 长方体
C、
长方体
C、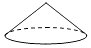 圆锥
D、
圆锥
D、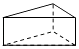 直三棱柱
4. 若二次根式 有意义,则x的取值范围是( )A、x≥ B、x≤ C、x≥ D、x≤5. 已知力F所作的功是15焦,则力F与物体在力的方向上通过的距离S的图象大致是如图中的( )A、
直三棱柱
4. 若二次根式 有意义,则x的取值范围是( )A、x≥ B、x≤ C、x≥ D、x≤5. 已知力F所作的功是15焦,则力F与物体在力的方向上通过的距离S的图象大致是如图中的( )A、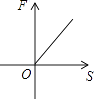 B、
B、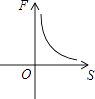 C、
C、 D、
D、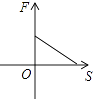 6. 如图,平行线a、b被直线c所截,若∠1=50°,则∠2的度数是( )
6. 如图,平行线a、b被直线c所截,若∠1=50°,则∠2的度数是( ) A、150° B、130° C、110° D、100°7. 如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )
A、150° B、130° C、110° D、100°7. 如图,现有一圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( )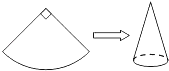 A、4cm B、3cm C、2cm D、1cm8. 在平面直角坐标系内,把抛物线y=(x﹣1)2+3向下平移2个单位,那么所得抛物线的解析式是( )A、y=(x﹣3)2 B、y=(x+1)2 C、y=(x﹣1)2+5 D、y=(x﹣1)2+19. α为锐角,且关于x的一元二次方程 有两个相等的实数根,则α=( )A、30° B、45° C、30°或150° D、60°10. 如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( )
A、4cm B、3cm C、2cm D、1cm8. 在平面直角坐标系内,把抛物线y=(x﹣1)2+3向下平移2个单位,那么所得抛物线的解析式是( )A、y=(x﹣3)2 B、y=(x+1)2 C、y=(x﹣1)2+5 D、y=(x﹣1)2+19. α为锐角,且关于x的一元二次方程 有两个相等的实数根,则α=( )A、30° B、45° C、30°或150° D、60°10. 如图,AB是⊙O的直径,弦CD⊥AB于H,若BH=2,CD=8,则⊙O的半径长为( ) A、2 B、3 C、4 D、511. 在正方形网格中,网格线的交点称为格点.如图是3×3的正方形网格,已知A,B是两格点,在网格中找一点C,使得△ABC为等腰直角三角形,则这样的点C有( )
A、2 B、3 C、4 D、511. 在正方形网格中,网格线的交点称为格点.如图是3×3的正方形网格,已知A,B是两格点,在网格中找一点C,使得△ABC为等腰直角三角形,则这样的点C有( ) A、6个 B、7个 C、8个 D、9个12. 如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE= ,那么重叠部分△AEF的面积为( )
A、6个 B、7个 C、8个 D、9个12. 如图,矩形纸片ABCD中,AB=3cm,现将纸片折叠压平,使点A与点C重合,折痕为EF,如果sin∠BAE= ,那么重叠部分△AEF的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
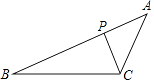
13. 分解因式:9﹣a2= .14. 如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:(写出一个即可).
 15. 如图,在⊙O中,若∠BAC=43°,则∠BOC=°.
15. 如图,在⊙O中,若∠BAC=43°,则∠BOC=°.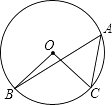 16. 如图,△ABC中,AB=AC=5,BC=6,AE平分∠BAC交BC于点E,点D为AB的中点,连结DE,则△BDE的周长是 .
16. 如图,△ABC中,AB=AC=5,BC=6,AE平分∠BAC交BC于点E,点D为AB的中点,连结DE,则△BDE的周长是 .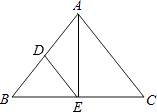 17. 如图,在▱ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于 .
17. 如图,在▱ABCD中,DB=DC,∠C的度数比∠ABD的度数大54°,AE⊥BD于点E,则∠DAE的度数等于 . 18. 如图,点A1 , A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1 , A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是 .
18. 如图,点A1 , A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1 , A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是 .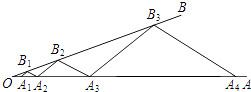
三、解答题
-
19. 化简求值: ,其中x= .20. 某市公租房倍受社会关注,2012年竣工的公租房有A,B,C,D 四种型号共500套,B型号公租房的入住率为40%.A,B,C,D 四种型号竣工的套数及入住的情况绘制了图1和图2两幅尚不完整的统计图.
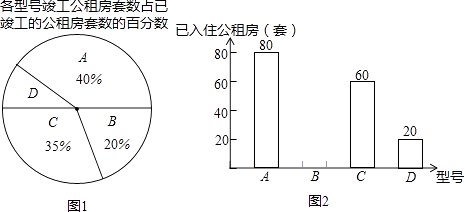 (1)、请你将图1和图2的统计图补充完整;(2)、在安置中,由于D型号公租房很受欢迎,入住率很高,2012年竣工的D型公租房中,仅有5套没有入住,其中有两套在同一单元同一楼层,其余3套在不同的单元不同的楼层.老王和老张分别从5套中各任抽1套,用树状图或列表法求出老王和老张住在同一单元同一楼层的概率.21. 如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
(1)、请你将图1和图2的统计图补充完整;(2)、在安置中,由于D型号公租房很受欢迎,入住率很高,2012年竣工的D型公租房中,仅有5套没有入住,其中有两套在同一单元同一楼层,其余3套在不同的单元不同的楼层.老王和老张分别从5套中各任抽1套,用树状图或列表法求出老王和老张住在同一单元同一楼层的概率.21. 如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.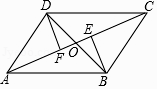 (1)、求证:△BOE≌△DOF;(2)、若OA= BD,则四边形ABCD是什么特殊四边形?请说明理由.22. 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E.
(1)、求证:△BOE≌△DOF;(2)、若OA= BD,则四边形ABCD是什么特殊四边形?请说明理由.22. 如图,PA为⊙O的切线,A为切点,过A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E. (1)、求证:PB为⊙O的切线;(2)、若tan∠ABE= ,求sin∠E.23. 甜甜水果批发商销售每箱进价为30元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若以每箱40元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.(1)、求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;(2)、求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;(3)、如果批发商平均每天获得的销售利润为1008元,那么每箱苹果的销售价是多少元?24. 如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.
(1)、求证:PB为⊙O的切线;(2)、若tan∠ABE= ,求sin∠E.23. 甜甜水果批发商销售每箱进价为30元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若以每箱40元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.(1)、求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式;(2)、求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式;(3)、如果批发商平均每天获得的销售利润为1008元,那么每箱苹果的销售价是多少元?24. 如图,已知二次函数y=ax2+bx+c的象经过A(﹣1,0)、B(3,0)、N(2,3)三点,且与y轴交于点C.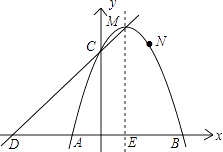 (1)、求这个二次函数的解析式,并写出顶点M及点C的坐标;(2)、若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;(3)、点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1)、求这个二次函数的解析式,并写出顶点M及点C的坐标;(2)、若直线y=kx+d经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;(3)、点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使以点P为圆心的圆经过A、B两点,并且与直线CD相切?如果存在,请求出点P的坐标;如果不存在,请说明理由.