2017年山东省日照市中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 计算(﹣2)0+9÷(﹣3)的结果是( )A、﹣1 B、﹣2 C、﹣3 D、﹣42. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、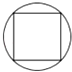 3. 如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )
3. 如图,几何体是由底面圆心在同一条直线上的三个圆柱构成的,其俯视图是( )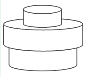 A、
A、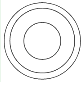 B、
B、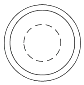 C、
C、 D、
D、 4. 下列运算正确的是( )A、3﹣1=﹣3 B、 =±3 C、(ab2)3=a3b6 D、a6÷a2=a35. 某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是( )A、30,27 B、30,29 C、29,30 D、30,286. 某生态示范园,计划种植一批核桃,原计划总产量达36千克,为了满足市场需求,现决定改良核桃品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各为多少万千克?设原计划每亩平均产量x万千克,则改良后平均亩产量为1.5x万千克.根据题意列方程为( )A、 ﹣ =20 B、 ﹣ =20 C、 ﹣ =20 D、 + =207. 将下列多项式因式分解,结果中不含有因式a+1的是( )A、a2﹣1 B、a2+a C、a2+a﹣2 D、(a+2)2﹣2(a+2)+18. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
4. 下列运算正确的是( )A、3﹣1=﹣3 B、 =±3 C、(ab2)3=a3b6 D、a6÷a2=a35. 某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是( )A、30,27 B、30,29 C、29,30 D、30,286. 某生态示范园,计划种植一批核桃,原计划总产量达36千克,为了满足市场需求,现决定改良核桃品种,改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万千克,种植亩数减少了20亩,则原计划和改良后平均每亩产量各为多少万千克?设原计划每亩平均产量x万千克,则改良后平均亩产量为1.5x万千克.根据题意列方程为( )A、 ﹣ =20 B、 ﹣ =20 C、 ﹣ =20 D、 + =207. 将下列多项式因式分解,结果中不含有因式a+1的是( )A、a2﹣1 B、a2+a C、a2+a﹣2 D、(a+2)2﹣2(a+2)+18. 如图,在▱ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )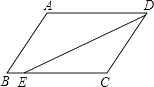 A、2cm B、4cm C、6cm D、8cm9. 若关于x的方程 + =3的解为正数,则m的取值范围是( )A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣10. 如图,在反比例函数y= (x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( )
A、2cm B、4cm C、6cm D、8cm9. 若关于x的方程 + =3的解为正数,则m的取值范围是( )A、m< B、m< 且m≠ C、m>﹣ D、m>﹣ 且m≠﹣10. 如图,在反比例函数y= (x>0)的图象上,有点P1 , P2 , P3 , P4 , 它们的横坐标依次为1,2,3,4,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1 , S2 , S3 , 则S1+S2+S3=( ) A、1 B、 C、 D、211.
A、1 B、 C、 D、211.如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C﹣D﹣E上移动,若点C,D,E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
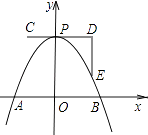 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
12. 今日,记者从潍坊市统计局获悉,2016年第一季度潍坊全市实现生产总值1256.77亿元,将1256.77亿用科学记数法可表示为(精确到百亿位) .13. 若3x2nym与x4﹣nyn﹣1是同类项,则m+n= .14. 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为 .
 15. 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示)
15. 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示)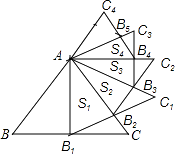
三、解答题
-
16. 综合题。(1)、先化简,再求代数式的值( + )÷ ,其中a=(﹣1)2012+tan60°.(2)、关于x的方程3x2+mx﹣8=0有一个根是 ,求另一个根及m的值.17. 某中学在实施快乐大课间之前组织过“我最喜欢的球类”的调查活动,每个学生仅选择一项,通过对学生的随机抽样调查得到一组数据,如图是根据这组数据绘制成的不完整统计图.
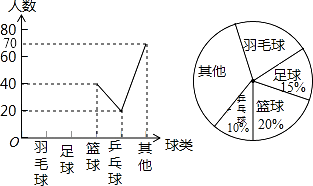 (1)、求出被调查的学生人数;(2)、把折线统计图补充完整;(3)、小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?18. AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
(1)、求出被调查的学生人数;(2)、把折线统计图补充完整;(3)、小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.如果确定小亮打第一场,其余三人用“手心、手背”的方法确定谁获胜谁打第一场若三人中有一人出的与其余两人不同则获胜;若三人出的都相同则平局.已知大刚出手心,请用树状图分析大刚获胜的概率是多少?18. AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.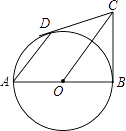
①求证:DC为⊙O切线;
②若AD•OC=8,求⊙O半径r.
19.菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
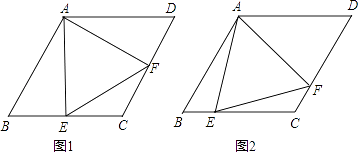 (1)、如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)、如图2,若∠EAF=60°,求证:△AEF是等边三角形.20. 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
(1)、如图1,若E是BC的中点,∠AEF=60°,求证:BE=DF;(2)、如图2,若∠EAF=60°,求证:△AEF是等边三角形.20. 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植﹣亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.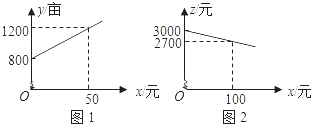 (1)、在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?(2)、分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;(3)、要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.21. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.
(1)、在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?(2)、分别求出政府补贴政策实施后,种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式;(3)、要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?并求出总收益w的最大值.21. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E、B.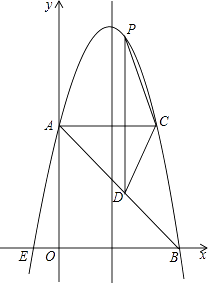 (1)、求二次函数y=ax2+bx+c的表达式;(2)、过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)、若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.
(1)、求二次函数y=ax2+bx+c的表达式;(2)、过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;(3)、若点M在抛物线上,点N在其对称轴上,使得以A、E、N、M为顶点的四边形是平行四边形,且AE为其一边,求点M、N的坐标.