2017年高考真题分类汇编(理数):专题6 立体几何
试卷更新日期:2017-07-20 类型:二轮复习
一、单选题
-
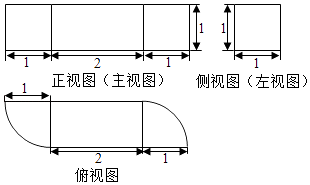
1. 某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )
 A、+1 B、+3 C、+1 D、+32. 如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, = =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( )
A、+1 B、+3 C、+1 D、+32. 如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, = =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,D﹣QR﹣P的平面角为α、β、γ,则( ) A、γ<α<β B、α<γ<β C、α<β<γ D、β<γ<α3. 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A、γ<α<β B、α<γ<β C、α<β<γ D、β<γ<α3. 某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( ) A、3 B、2 C、2 D、24. 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
A、3 B、2 C、2 D、24. 某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )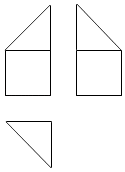 A、10 B、12 C、14 D、165. 已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )A、 B、 C、 D、6. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
A、10 B、12 C、14 D、165. 已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为( )A、 B、 C、 D、6. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )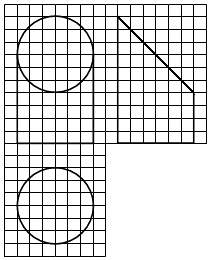 A、90π B、63π C、42π D、36π7. 已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A、π B、 C、 D、
A、90π B、63π C、42π D、36π7. 已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A、π B、 C、 D、二、填空题
-
8. 由一个长方体和两个 圆柱体构成的几何体的三视图如图,则该几何体的体积为 .
 9. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 .10. 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1 , 球O的体积为V2 , 则 的值是 .
9. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 .10. 如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1 , 球O的体积为V2 , 则 的值是 .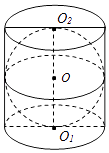 11. 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .
11. 如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为 .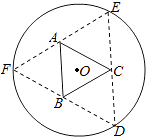 12. a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
12. a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最小值为60°;
其中正确的是(填写所有正确结论的编号)
三、解答题
-
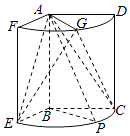
13. 如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 的中点.
(Ⅰ)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.
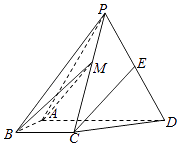
 14. 如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
14. 如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.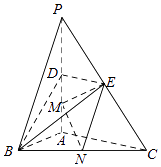
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C﹣EM﹣N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为 ,求线段AH的长.
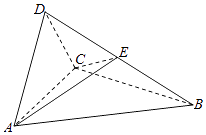
15. 如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
 16. 如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD= ,AB=4.
16. 如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD= ,AB=4.
(1)、求证:M为PB的中点;
(2)、求二面角B﹣PD﹣A的大小;(3)、求直线MC与平面BDP所成角的正弦值.
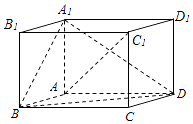
17. 如图,在平行六面体ABCD﹣A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1= ,∠BAD=120°.(Ⅰ)求异面直线A1B与AC1所成角的余弦值;
(Ⅱ)求二面角B﹣A1D﹣A的正弦值.
 18. 如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
18. 如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.
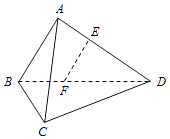 19. 如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
19. 如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.