2017年山东省日照市五莲县中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题

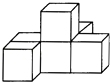
1. 数a的相反数是（）

A、|a| B、 $\frac{1}{a}$ C、﹣a D、 $\sqrt{a}$

查看试题解析
2. 如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、（ $\frac{1}{3}$ ）^﹣²=﹣9 B、 $\sqrt{4}$ =±2 C、﹣2（a﹣b）=﹣2a﹣2b D、ab⁴÷（﹣ab）=﹣b³

查看试题解析
4. 如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．则∠ABD的度数是（）

A、30° B、25° C、20° D、15°

查看试题解析
5. 我国计划在2020年左右发射火星探测卫星，据科学研究，火星距离地球的最近距离约为5500万千米，这个数据用科学记数法可表示为（）

A、5.5×10⁶千米 B、5.5×10⁷千米 C、55×10⁶千米 D、0.55×10⁸千米

查看试题解析
6. 关于x的一元二次方程x²﹣3x+m=0有两个不相等的实数根，则实数m的取值范围为（）

A、 $m > \frac{9}{4}$ B、 $m < \frac{9}{4}$ C、 $m = \frac{9}{4}$ D、 $m < - \frac{9}{4}$

查看试题解析
7. 2015年日照市人民政府投入1000万元用于改造乡村小学班班通工程建设，计划到2017年再追加投资210万元，如果每年的平均增长率相同，那么我市这两年该项投入的平均增长率为（）

A、1.21% B、8% C、10% D、12.1%

查看试题解析
8. 如果不等式组 $\{\begin{matrix} x > a \\ x < 2 \end{matrix}$ 恰有3个整数解，则a的取值范围是（　　）

A、a≤﹣1 B、a＜﹣1 C、﹣2≤a＜﹣1 D、﹣2＜a≤﹣1

查看试题解析
9. 如图，在四边形ABCD中，∠ABC=90°，AB=BC=2 $\sqrt{2}$ ，E、F分别是AD、CD的中点，连接BE、BF、EF．若四边形ABCD的面积为6，则△BEF的面积为（）

A、2 B、 $\frac{9}{4}$ C、 $\frac{5}{2}$ D、3

查看试题解析
10. 如图，AB为半圆O的直径，CD切⊙O于点E，AD、BC分别切⊙O于A、B两点，AD与CD相交于D，BC与CD相交于C，连接OD、OC，对于下列结论：①OD²=DE•CD；②AD+BC=CD；③OD=OC；④S_梯形_ABCD=CD•OA；⑤∠DOC=90°；⑥若切点E在半圆上运动（A、B两点除外），则线段AD与BC的积为定值．其中正确的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
11. 已知二次函数y=ax²+bx+1（a＜0）的图象过点（1，0）和（x₁ ， 0），且﹣2＜x₁＜﹣1，下列5个判断中：①b＜0；②b﹣a＜0；③a＞b﹣1；④a＜﹣ $\frac{1}{2}$ ；⑤2a＜b+ $\frac{1}{2}$ ，正确的是（）

A、①③ B、①②③ C、①②③⑤ D、①③④⑤

查看试题解析

二、填空题

12. 因式分解：﹣2x²y+8xy﹣6y= ．

查看试题解析
13. 求1+2+2²+2³+…+2²⁰¹⁷的值，可令S=1+2+2²+2³+…+2²⁰¹⁷ ，则2S=2+2²+2³+…+2²⁰¹⁸ ，因此2S﹣S=2²⁰¹⁸﹣1，仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁷的值为．

查看试题解析
14.
如图：在x轴的上方，直角∠BOA绕原点O顺时针方向旋转，若∠BOA的两边分别与函数y=﹣ $\frac{1}{x}$ 、y= $\frac{2}{x}$ 的图象交于B、A两点，则tanA= ．

查看试题解析
15.
如图四边形ABCD中，AD=DC，∠DAB=∠ACB=90°，过点D作DF⊥AC，垂足为F．DF与AB相交于E．设AB=15，BC=9，P是射线DF上的动点．当△BCP的周长最小时，DP的长为．

查看试题解析

三、解答题

16. 综合题。

(1)、解不等式组 ${\begin{matrix} 3 (x + 1) > 4 x + 2 \\ \frac{x}{2} > \frac{x - 1}{3} \end{matrix}$ ，并写出不等式组的整数解．

(2)、化简分式：（ $\frac{3 x}{x - 1}$ ﹣ $\frac{x}{x + 1}$ ）÷ $\frac{x}{x^{2} - 1}$ ，再从﹣2＜x＜3的范围内选取一个你最喜欢的值代入求值．

查看试题解析
17. 如图，已知△ABC中，AB=AC，把△ABC绕A点沿顺时针方向旋转得到△ADE，连接BD，CE交于点F．

(1)、求证：△AEC≌△ADB；

(2)、若AB=2，∠BAC=45°，当四边形ADFC是菱形时，求BF的长．

查看试题解析
18. 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息，解答下列问题：

(1)、a= ， b= ，且补全频数分布直方图；

(2)、若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？

(3)、在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．

查看试题解析
19. 骑自相车旅行越来越受到人们的喜爱，顺风车行经营的A型车2016年4月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售比去年增加400元，若今年4月份与去年4月份卖出的A型车数量相同，则今年4月份A型车销售总额将比去年4月份销售总额增加25%．

(1)、求今年4月份A型车每辆销售价多少元（用列方程的方法解答）；

(2)、该车行计划5月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A、B两种型号车的进货和销售价格如表：
A型车
B型车
进货价格（元/辆）
1100
1400
销售价格（元/辆）
今年的销售价格
2400

查看试题解析
20.
爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AM⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．

(1)、如图1，当tan∠PAB=1，c=4 $\sqrt{2}$ 时，a= ， b=；
如图2，当∠PAB=30°，c=2时，a= ， b=；

(2)、请你观察（1）中的计算结果，猜想a²、b²、c²三者之间的关系，用等式表示出来，并利用图3证明你的结论．

(3)、如图4，▱ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 $\sqrt{5}$ ，AB=3，求AF的长．

查看试题解析
21.
已知抛物线y=a（x+3）（x﹣1）（a≠0），与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线y=﹣ $\sqrt{3}$ x+b与抛物线的另一个交点为D．

(1)、若点D的横坐标为2，求抛物线的函数解析式；

(2)、若在第三象限内的抛物线上有点P，使得以A、B、P为顶点的三角形与△ABC相似，求点P的坐标；

(3)、在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒 $\frac{2 \sqrt{3}}{3}$ 个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？

查看试题解析

获奖等次	频数	频率
一等奖	10	0.05
二等奖	20	0.10
三等奖	30	b
优胜奖	a	0.30
鼓励奖	80	0.40

	A型车	B型车
进货价格（元/辆）	1100	1400
销售价格（元/辆）	今年的销售价格	2400