2017年云南省昆明市官渡区中考数学二模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、填空题

1. ﹣3的绝对值是．

查看试题解析
2. 函数y= $\frac{x}{x - 2}$ 的自变量x取值范围是．

查看试题解析
3. 如图，在△ABC中，AB=AC，边AB的垂直平分线MN交AC于点D，若△BCD的周长为24cm，BC=10cm，则AB的长为 cm．

查看试题解析
4. 如图，AB、CD相交于点O，OC=4，OD=6，AC∥BD，EF是△ODB的中位线，且EF=4，则AC的长为．

查看试题解析
5. 用一个圆心角为90°半径为16cm的扇形做成一个圆锥的侧面（接缝处不重叠），则这个圆锥底面圆的半径为 cm．

查看试题解析
6. 如图有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，第4幅图中有7个菱形，第n（n是正整数）幅图中共有个菱形．

查看试题解析

二、选择题

7. ﹣ $\frac{2}{3}$ 的倒数是（）

A、 $\frac{2}{3}$ B、﹣ $\frac{3}{2}$ C、﹣ $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
8. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案，下图中我国四大银行的商标图案中既是轴对称图形又是中心对称图形的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. H7N9禽流感病毒的直径大约为0.0000000805米，这个数用科学记数法表示为（）

A、8.05×10^﹣8 B、8.05×10^﹣7 C、80.5×10^﹣9 D、0.805×10^﹣7

查看试题解析
10. 下列运算正确的是（）

A、（﹣ $\frac{3}{2}$ ）²=﹣ $\frac{9}{4}$ B、（3a²）³=9a⁶ C、5^﹣3÷5^﹣5= $\frac{1}{25}$ D、 $\sqrt{8} - \sqrt{50} = - 3 \sqrt{2}$

查看试题解析
11.
在2014年的体育中考中，某校6名学生的体育成绩统计如图，则这组数据的众数、中位数、方差依次是（）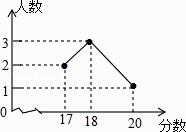

A、18，18，1 B、18，17.5，3 C、18，18，3 D、18，17.5，1

查看试题解析
12. 化简 $\frac{a^{2} - b^{2}}{a^{2} + a b}$ 的结果为（）

A、 $- \frac{b}{a}$ B、 $\frac{a - b}{a}$ C、 $\frac{a + b}{a}$ D、﹣b

查看试题解析
13. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、560（1+x）²=315 B、560（1﹣x）²=315 C、560（1﹣2x）²=315 D、560（1﹣x²）=315

查看试题解析
14. 已知⊙O是△ABC的外接圆，边BC=4cm，且⊙O半径也为4cm，则∠A的度数是（）

A、30° B、60°或120° C、150° D、30°或150°

查看试题解析

三、解答题

15. 解分式方程： $\frac{1}{x - 3} + \frac{x}{3 - x} = 2$

查看试题解析
16. 我市某中学为了深入学习社会主义核心价值观，特对本校部分学生（随机抽样）进行了一次相关知识的测试（成绩分为A、B、C、D、E五个组，x表示测试成绩），A组：90≤x≤100 B组：80≤x＜90 C组：70≤x＜80 D组：60≤x＜70 E组：x＜60；通过对测试成绩的分析，得到如图所示的两幅不完整的统计图，请你根据图中提供的信息解答以下问题．

(1)、填空：参加调查测试的学生共有人；A组所占的百分比为，在扇形统计图中，C组所在扇形的圆心角为度；

(2)、请将条形统计图补充完整．

(3)、本次调查测试成绩在80分以上（含80分）为优秀，该中学共有3000人，请估计全校测试成绩为优秀的学生有多少人？

查看试题解析
17. 如图，矩形ABCD中，AB=8，AD=6，点E、F分别在边CD、AB上．

(1)、若DE=BF，求证：四边形AFCE是平行四边形；

(2)、若四边形AFCE是菱形，求菱形AFCE的周长．

查看试题解析
18. 如图，直线y=mx+n与双曲线y= $\frac{k}{x}$ 相交于A（﹣1，2），B（2，b）两点，与y轴相交于点C．

(1)、求m，n的值；

(2)、若点D与点C关于x轴对称，求△ABD的面积．

查看试题解析
19. 已知有甲、乙两个不透明的袋子，甲袋内装有标记数字﹣1，2，3的三张卡片，乙袋内装有标记数字2，3，4的三张卡片（卡片除数字不同其余都相同）．先从甲袋中随机抽取一张卡片，记录下数字，再从乙袋中随机抽取一张卡片，记录下数字．

(1)、利用列表或画树状图的方法（只选其中一种）表示出所抽两张卡片上数字之积所有可能的结果：

(2)、求抽出的两张卡片上的数字之积是3的倍数的概率．

查看试题解析
20.
如图，在电线杆上的C处引拉线CE、CF固定电线杆，拉线CE和地面所成的角∠CED=60°，在离电线杆6米的B处安置测角仪AB，在A处测得电线杆上C处的仰角为30°，已知测角仪高AB为1.5米，求拉线CE的长（结果精确到0.1米，参考数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）．

查看试题解析
21. 某体育用品商场采购员要到厂家批发购进篮球和排球共100只，付款总额不得超过11 815元．已知两种球厂家的批发价和商场的零售价如右表，试解答下列问题：
品名
厂家批发价（元/只）
市场零售价（元/只）
篮球
130
160
排球
100
120

(1)、该采购员最多可购进篮球多少只？

(2)、若该商场把这100只球全部以零售价售出，为使商场获得的利润不低于2580元，则采购员至少要购篮球多少只，该商场最多可盈利多少元？

查看试题解析
22. 如图，在△ABC中，AB=BC，D是AC中点，BE平分∠ABD交AC于点E，点O是AB上一点，⊙O过B、E两点，交BD于点G，交AB于点F．

(1)、判断直线AC与⊙O的位置关系，并说明理由；

(2)、当BD=6，AB=10时，求⊙O的半径．

查看试题解析
23.
如图，在平面直角坐标系中，抛物线y=ax²+6x+c（a≠0）交y轴于A点，交x轴于B、C两点（点B在点C的左侧），已知A点坐标为（0，﹣5），点B的坐标为（1，0）．

(1)、求此抛物线的解析式及定点坐标；

(2)、过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C的位置关系，并说明理由；

(3)、在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析

品名	厂家批发价（元/只）	市场零售价（元/只）
篮球	130	160
排球	100	120