2017年四川省绵阳市游仙区中考数学模拟试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1.
的倒数是( )
A、﹣ B、 C、﹣ D、2. 在下列四个汽车标志图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、a2•a4=a8 D、(﹣a3)2=a64. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣65. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
3. 下列运算正确的是( )A、 B、 C、a2•a4=a8 D、(﹣a3)2=a64. PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣65. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、
B、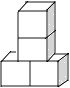 C、
C、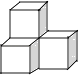 D、
D、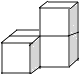 6.
6.如图,一次函数y=(m﹣1)x﹣3的图象分别与x轴、y轴的负半轴相交于A、B,则m的取值范围是( )
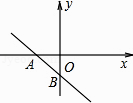 A、m>1 B、m<1 C、m<0 D、m>07. 三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的一个根,则这个三角形的周长是( )A、9 B、11 C、13 D、11或138. 如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )
A、m>1 B、m<1 C、m<0 D、m>07. 三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的一个根,则这个三角形的周长是( )A、9 B、11 C、13 D、11或138. 如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )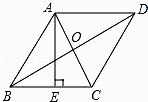 A、 cm B、 cm C、 cm D、5 cm9. 如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
A、 cm B、 cm C、 cm D、5 cm9. 如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )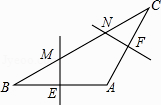 A、4cm B、3cm C、2cm D、1cm10.
A、4cm B、3cm C、2cm D、1cm10.如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
 A、
A、 B、
B、 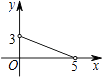 C、
C、 D、
D、 11. 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD//OB,则图中休闲区(阴影部分)的面积是( )
11. 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD//OB,则图中休闲区(阴影部分)的面积是( )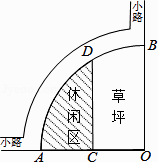 A、 B、 C、 D、12.
A、 B、 C、 D、12.图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),…,则第n个图形的周长是( )
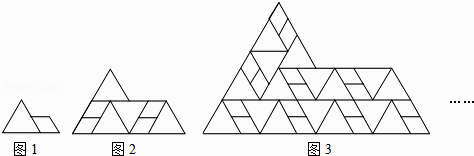 A、2n B、4n C、2n+1 D、2n+2
A、2n B、4n C、2n+1 D、2n+2二、填空题
-
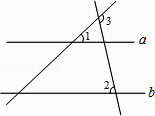
13. 已知 ,则 的值为 .14. 如图,a//b,∠1=40°,∠2=80°,则∠3=度.
 15. 分解因式:a2b﹣4b3= .16. 某市举办“体彩杯”中学生篮球赛,初中男子组有市直学校的A、B、C三个队和县区学校的D,E,F,G,H五个队,如果从A,B,D,E四个队与C,F,G,H四个队中个抽取一个队进行首场比赛,那么首场比赛出场的两个队都是县区学校队的概率是 .17.
15. 分解因式:a2b﹣4b3= .16. 某市举办“体彩杯”中学生篮球赛,初中男子组有市直学校的A、B、C三个队和县区学校的D,E,F,G,H五个队,如果从A,B,D,E四个队与C,F,G,H四个队中个抽取一个队进行首场比赛,那么首场比赛出场的两个队都是县区学校队的概率是 .17.如图,四边形ABCD是等腰梯形,∠ABC=60°,若其四边满足长度的众数为5,平均数为 ,上、下底之比为1:2,则BD= .
 18. 如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .
18. 如图,在△ABC中,4AB=5AC,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.若点H是AC的中点,则 的值为 .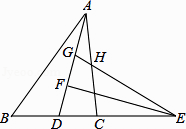
三、解答题
-
19. 计算题(1)、求值:2 sin45°+(﹣3)2﹣20170×|﹣4|+ ;(2)、先化简,再求值:( ﹣x﹣1)÷ ,其中x是不等式组 的一个整数解.20. 某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别
正常字数x
人数
A
0≤x<8
10
B
8≤x<16
15
C
16≤x<24
25
D
24≤x<32
m
E
32≤x<40
n
根据以上信息完成下列问题:
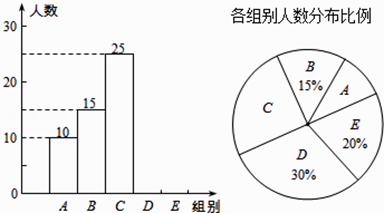 (1)、统计表中的m= , n= , 并补全条形统计图;(2)、扇形统计图中“C组”所对应的圆心角的度数是;(3)、已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.21. 如图,直线y=﹣x+b与反比例函数y= 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
(1)、统计表中的m= , n= , 并补全条形统计图;(2)、扇形统计图中“C组”所对应的圆心角的度数是;(3)、已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.21. 如图,直线y=﹣x+b与反比例函数y= 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB. (1)、求k和b的值;(2)、直接写出一次函数值小于反比例函数值的自变量x的取值范围;(3)、在y轴上是否存在一点P,使S△PAC= S△AOB?若存在请求出点P坐标,若不存在请说明理由.22. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)、求k和b的值;(2)、直接写出一次函数值小于反比例函数值的自变量x的取值范围;(3)、在y轴上是否存在一点P,使S△PAC= S△AOB?若存在请求出点P坐标,若不存在请说明理由.22. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.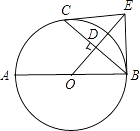 (1)、求证:BE与⊙O相切;(2)、连接AD并延长交BE于点F,若OB=9,sin∠ABC= ,求BF的长.23. 某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.(1)、求平均每分钟一个正门和一个侧门各可以通过多少名学生?(2)、检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.24. 如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°
(1)、求证:BE与⊙O相切;(2)、连接AD并延长交BE于点F,若OB=9,sin∠ABC= ,求BF的长.23. 某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.(1)、求平均每分钟一个正门和一个侧门各可以通过多少名学生?(2)、检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.24. 如图1,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°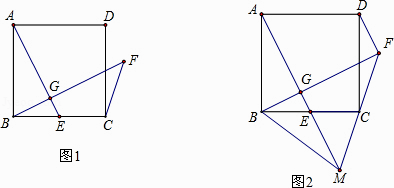 (1)、求证:AG=FG;(2)、如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.
(1)、求证:AG=FG;(2)、如图2延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=10,求FD的长.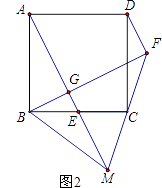 25.
25.如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.
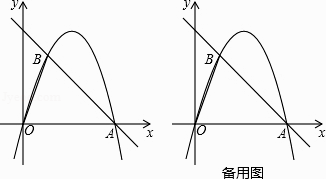 (1)、求a,b的值;(2)、点P是线段AB上一动点(点P不与点A、B重合),过点P作PM//OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR//MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
(1)、求a,b的值;(2)、点P是线段AB上一动点(点P不与点A、B重合),过点P作PM//OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);(3)、在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR//MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.