2017年四川省泸州市中考数学模拟试卷(5月份)
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 3的倒数是( )A、 B、﹣ C、 D、﹣32. 下列运算正确的是( )
A、a•a2=a2 B、(a2)3=a6 C、a2+a3=a6 D、a6÷a2=a33. 下列标志既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 今年1~2月,我市完成固定资产投资201.4亿元,增速21%,高于全省平均增速8.6个百分点,增速继续保持全省第一,数据201.4亿用科学记数法表示为( )A、201.4×108 B、2.014×108 C、2.014×109 D、2.014×10105. 如图所示的三棱柱的主视图是( )
4. 今年1~2月,我市完成固定资产投资201.4亿元,增速21%,高于全省平均增速8.6个百分点,增速继续保持全省第一,数据201.4亿用科学记数法表示为( )A、201.4×108 B、2.014×108 C、2.014×109 D、2.014×10105. 如图所示的三棱柱的主视图是( ) A、
A、 B、
B、 C、
C、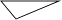 D、
D、 6. 为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:
6. 为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:居民(户)
1
3
2
4
月用电量(度/户)
40
50
55
60
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A、中位数是55 B、众数是60 C、方差是29 D、平均数是547. 若不等式组 的解集为0<x<1,则a、b的值分别为( )A、a=2,b=1 B、a=2,b=3 C、a=﹣2,b=3 D、a=﹣2,b=18. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,点D到AB的距离DE=1cm,BE= cm,则BC等于( )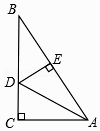 A、1cm B、2cm C、3cm D、( +1)cm9. 方程(m﹣2)x2﹣ x+ =0有两个实数根,则m的取值范围( )A、m> B、m≤ 且m≠2 C、m≥3 D、m≤3且m≠210. 如图,⊙O中,弦AB的长为6cm,圆心O到AB的距离为4cm,则⊙O的半径长为( )
A、1cm B、2cm C、3cm D、( +1)cm9. 方程(m﹣2)x2﹣ x+ =0有两个实数根,则m的取值范围( )A、m> B、m≤ 且m≠2 C、m≥3 D、m≤3且m≠210. 如图,⊙O中,弦AB的长为6cm,圆心O到AB的距离为4cm,则⊙O的半径长为( ) A、3cm B、4cm C、5cm D、6cm11. 如图,菱形ABCD的周长为8cm,高AE长为 cm,则对角线AC长和BD长之比为( )
A、3cm B、4cm C、5cm D、6cm11. 如图,菱形ABCD的周长为8cm,高AE长为 cm,则对角线AC长和BD长之比为( ) A、1:2 B、1:3 C、1: D、1:12. 如图,点A(3,m)在双曲线 上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( )
A、1:2 B、1:3 C、1: D、1:12. 如图,点A(3,m)在双曲线 上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( ) A、6 B、5 C、4 D、3
A、6 B、5 C、4 D、3二、填空题
-
13. 分解因式:ab2﹣a3= .14. 已知,ab=﹣1,a+b=2,则式子 + = .15. 已知关于x的方程(a+2)x2﹣2ax+a=0有两个不相等的实数根x1和x2 , 抛物线y=x2﹣(2a+1)x+2a﹣5与x轴的两个交点分别为位于点(2,0)的两旁,若|x1|+|x2|=2 ,则a的值为 .16. 如图,在平面直角坐标系中,已知点A、B、C的坐标分别为(﹣1,0),(5,0),(0,2).若点P从A点出发,沿x轴正方向以每秒1个单位长度的速度向B点移动,连接PC并延长到点E,使CE=PC,将线段PE绕点P顺时针旋转90°得到线段PF,连接FB.若点P在移动的过程中,使△PBF成为直角三角形,则点F的坐标是 .

三、本大题
-
17. 计算:﹣ +|﹣ |×sin45°+(π﹣1)0﹣ .18. 如图,在▱ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
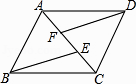 19. 先化简,再求值:(x﹣4+ )÷( ﹣1),其中x=2﹣ .20. 为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.
19. 先化简,再求值:(x﹣4+ )÷( ﹣1),其中x=2﹣ .20. 为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图.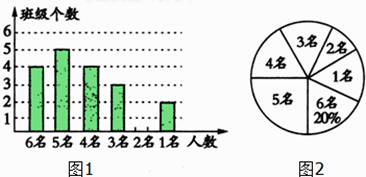 (1)、求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;(2)、该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.21. 某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.(1)、求出A型、B型污水处理设备的单价;(2)、经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.22. 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ≈1.732)
(1)、求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;(2)、该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.21. 某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.(1)、求出A型、B型污水处理设备的单价;(2)、经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.22. 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ≈1.732)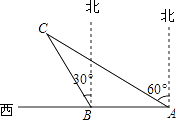 23. 如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数 (k为不等于0的常数)的图象在第一象限交于点A(1,n).求:
23. 如图.一次函数y=x+b的图象经过点B(﹣1,0),且与反比例函数 (k为不等于0的常数)的图象在第一象限交于点A(1,n).求: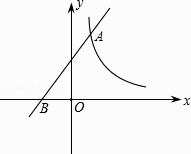 (1)、一次函数和反比例函数的解析式;(2)、当1≤x≤6时,反比例函数y的取值范围.24. 如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP,
(1)、一次函数和反比例函数的解析式;(2)、当1≤x≤6时,反比例函数y的取值范围.24. 如图1,已知矩形ABCD,E为AD边上一动点,过A,B,E三点作⊙O,P为AB的中点,连接OP,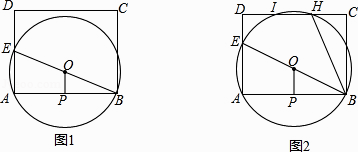 (1)、求证:BE是⊙O的直径且OP⊥AB;(2)、若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;(3)、如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.25. 如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)、求证:BE是⊙O的直径且OP⊥AB;(2)、若AB=BC=8,AE=6,试判断直线DC与⊙O的位置关系,并说明理由;(3)、如图2,若AB=10,BC=8,⊙O与DC边相交于H,I两点,连结BH,当∠ABE=∠CBH时,求△ABE的面积.25. 如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.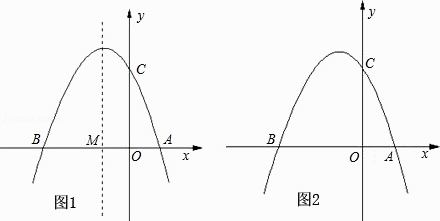 (1)、求抛物线的解析式;(2)、设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
(1)、求抛物线的解析式;(2)、设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;(3)、如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.