2017年四川省达州市渠县五校联合中考数学三模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题:
-
1. 如果a与3互为相反数,则 是( )A、3 B、﹣3 C、 D、﹣2. 下列运算正确的是( )A、a2•a3=a5 B、(a2)3=a5 C、 D、a5+a5=a103. 下图是由5个相同大小的正方体搭成的几何体,则它的俯视图在A,B,C,D中的选项是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 已知二次函数y=kx2﹣6x+3,若k在数组(﹣3,﹣2,﹣1,1,2,3,4)中随机取一个,则所得抛物线的对称轴在直线x=1的右方时的概率为( )A、 B、 C、 D、5. 为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )A、600 m2 B、625 m2 C、650 m2 D、675 m26. 已知不等式(a+1)x>2的解集是x<﹣1,则( )A、a>2 B、a≤﹣3 C、a=3 D、a=﹣37. 函数y=kx+b与函数y= 在同一坐标系中的大致图象正确的是( )A、
4. 已知二次函数y=kx2﹣6x+3,若k在数组(﹣3,﹣2,﹣1,1,2,3,4)中随机取一个,则所得抛物线的对称轴在直线x=1的右方时的概率为( )A、 B、 C、 D、5. 为搞好环保,某公司准备修建一个长方体的污水处理池,池底矩形的周长为100m,则池底的最大面积是( )A、600 m2 B、625 m2 C、650 m2 D、675 m26. 已知不等式(a+1)x>2的解集是x<﹣1,则( )A、a>2 B、a≤﹣3 C、a=3 D、a=﹣37. 函数y=kx+b与函数y= 在同一坐标系中的大致图象正确的是( )A、 B、
B、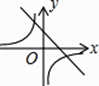 C、
C、 D、
D、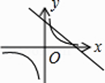 8. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( )
8. 如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) A、10 B、8 C、4 D、29.
A、10 B、8 C、4 D、29.如图,在矩形ABCD中,有一个菱形BFDE(点E、F分别在线段AB、CD上),记它们的面积分别为SABCD和SBFDE . 现给出下列命题:
(i)若 = ,则tan∠EDF=
(ii)若DE2=BD•EF,则DF=2AD
那么,下面判断正确的是( )
 A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误10. 如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )
A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误10. 如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1 , 将C1向右平移得C2 , C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是( )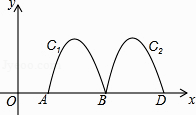 A、﹣2<m< B、﹣3<m<﹣ C、﹣3<m<﹣2 D、﹣3<m<﹣
A、﹣2<m< B、﹣3<m<﹣ C、﹣3<m<﹣2 D、﹣3<m<﹣二、填空题:
-
11. 234 610 000用科学记数法表示为 . (保留三个有效数字)12. 已知:x2﹣2x+1+ =0,则|x﹣y|= .13. 若方程kx2﹣6x+1=0有两个实数根,则k的取值范围是 .14. 将二次函数y=(x﹣2)2+3的图象向右平移3个单位,再向下平移2个单位,所得二次函数的解析式为 .15. 在□a2□2ab□b2的三个空格中,顺次填上“+”或“﹣”,恰好能构成完全平方式的概率是 .
16. 已知抛物线y=x2+bx+c的顶点在x轴上;点A(m,9).B(m+n,9)在它图象上,则:n= .三、解答题
-
17. 计算: ﹣(﹣1)2015×(﹣ )﹣2﹣|1﹣ |18. 解方程: = +2.19. 一个不透明的口袋里装有红、黄、绿三种颜色的小球(除颜色不同外其余都相同),其中红球2个(分别标有1号、2号),黄球1个,从中任意摸出1球是绿球的概率是 .(1)、试求口袋中绿球的个数;(2)、小明和小刚玩摸球游戏:第一次从口袋中任意摸出1球(不放回),第二次再摸出1球.两人约定游戏胜负规则如下:摸出“一绿一黄”,则小明赢;摸出“一红一黄”,则小刚赢.你认为这种游戏胜负规则公平吗?请用列表或画树状图的方法说明理由;若你认为不公平,请修改游戏胜负规则,使游戏变得公平.20. 如图,有两条公路OM、ON相交成30°角,沿公路OM方向离O点80米处有一所学校A.当重型运输卡车P沿道路ON方向行驶时,在以P为圆心50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿道路ON方向行驶的速度为18千米/时.
 (1)、求对学校A的噪声影响最大时卡车P与学校A的距离;(2)、求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.21. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?22. 已知关于x的方程x2﹣2(k﹣3)x+k2﹣4k﹣1=0的两实数根之和不小于﹣6(1)、求k的取值范围;(2)、若以方程x2﹣2(k﹣3)x+k2﹣4k﹣1=0的两个根为横坐标、纵坐标的点恰在反比例函数y= 的图象上,求满足条件的m的取值范围.23. 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
(1)、求对学校A的噪声影响最大时卡车P与学校A的距离;(2)、求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间.21. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?22. 已知关于x的方程x2﹣2(k﹣3)x+k2﹣4k﹣1=0的两实数根之和不小于﹣6(1)、求k的取值范围;(2)、若以方程x2﹣2(k﹣3)x+k2﹣4k﹣1=0的两个根为横坐标、纵坐标的点恰在反比例函数y= 的图象上,求满足条件的m的取值范围.23. 如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC. (1)、当t为何值时,点Q与点D重合?(2)、当⊙Q经过点A时,求⊙P被OB截得的弦长.24.
(1)、当t为何值时,点Q与点D重合?(2)、当⊙Q经过点A时,求⊙P被OB截得的弦长.24.定义:有三个内角相等凸四边形叫三等角四边形.
 (1)、三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;(2)、如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.(3)、三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答)25.
(1)、三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;(2)、如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.(3)、三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答)25.已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4.
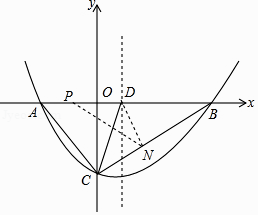 (1)、求该抛物线的解析式;(2)、点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PN被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点N的运动速度;若不存在,请说明理由;(3)、在(2)的结论下,直线x=1上是否存在点M使△MPN为等腰三角形?若存在,请直接写出所有点M的坐标;若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PN被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点N的运动速度;若不存在,请说明理由;(3)、在(2)的结论下,直线x=1上是否存在点M使△MPN为等腰三角形?若存在,请直接写出所有点M的坐标;若不存在,请说明理由.