2017年四川省达州市开江县中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣ 的相反数是( )A、2 B、﹣2 C、 D、﹣2. 宇宙现在的年龄约为200亿年,200亿用科学记数法表示为( )A、0.2×1011 B、2×1010 C、200×108 D、2×1093. 下列计算正确的是( )A、x4+x4=x16 B、(﹣2a)2=﹣4a2 C、x7÷x5=x2 D、m2•m3=m64.
如图是我国几家银行的标志,其中即是轴对称图形又是中心对称图形的有( )
 A、2个 B、3个 C、4个 D、5个5. 把不等式组 的解集表示在数轴上,正确的是( )A、
A、2个 B、3个 C、4个 D、5个5. 把不等式组 的解集表示在数轴上,正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 函数y= 的自变量x的取值范围是( )A、x≥﹣1 B、x≥﹣1且x≠2 C、x≠±2 D、x>﹣1且x≠27. 如图,是一个几何体的三视图,那么三视图所对应的几何体是( )
6. 函数y= 的自变量x的取值范围是( )A、x≥﹣1 B、x≥﹣1且x≠2 C、x≠±2 D、x>﹣1且x≠27. 如图,是一个几何体的三视图,那么三视图所对应的几何体是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为( )A、 = B、 = C、 = D、 =9.
8. A,B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运40千克,A型机器人搬运1200千克所用时间与B型机器人搬运800千克所用时间相等.设B型机器人每小时搬运化工原料x千克,根据题意可列方程为( )A、 = B、 = C、 = D、 =9.如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
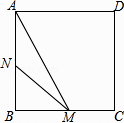 A、
A、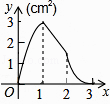 B、
B、 C、
C、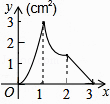 D、
D、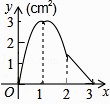 10. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )
10. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 分解因式:16m3﹣mn2 .12. 两组数据m,6,n与1,m,2n,7的平均数都是6,若将这两组数据合并成一组数据,则这组新数据的中位数为 .13. 从﹣2,﹣1,0,1,2这5个数中,随机抽取一个数记为a,则使关于x的不等式组 有解,且使关于x的一元一次方程 +1= 的解为负数的概率为 .14. 如图,点B、C把 分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是 .
 15.
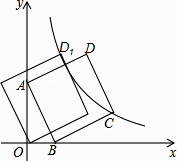
15.如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= (k≠0)上的点D1处,则a= .
 16. 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG//CF;⑤S△FGC=3.6.其中正确结论是 .
16. 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG//CF;⑤S△FGC=3.6.其中正确结论是 .
三、解答题
-
17. 计算:2sin45°﹣3﹣2+ +| ﹣2|+ .18. 先化简: ÷( ﹣ ),然后再从﹣2<x≤2的范围内选取一个合适的x的整数值代入求值.
四、解答题
-
19. 某校七年级(1)班班主任对本班学生进行了“我最喜欢的课外活动”的调查,并将调查结果分为书法和绘画类(记为A)、音乐类(记为B)、球类(记为C)、其它类(记为D).根据调查结果发现该班每个学生都进行了登记且每人只登记了一种自己最喜欢的课外活动.班主任根据调查情况把学生进行了归类,并制作了如下两幅统计图.请你结合图中所给信息解答下列问题:
 (1)、七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;(2)、学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名学生擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.20. 如图,反比例函数y= 的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y= 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
(1)、七年级(1)班学生总人数为人,扇形统计图中D类所对应扇形的圆心角为度,请补全条形统计图;(2)、学校将举行书法和绘画比赛,每班需派两名学生参加,A类4名学生中有两名学生擅长书法,另两名学生擅长绘画.班主任现从A类4名学生中随机抽取两名学生参加比赛,请你用列表或画树状图的方法求出抽到的两名学生恰好是一名擅长书法,另一名擅长绘画的概率.20. 如图,反比例函数y= 的图象经过点A(﹣1,4),直线y=﹣x+b(b≠0)与双曲线y= 在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点. (1)、求k的值;(2)、当b=﹣2时,求△OCD的面积;(3)、连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.
(1)、求k的值;(2)、当b=﹣2时,求△OCD的面积;(3)、连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.
五、解答题
-
21. 为迎接“国家卫生城市”复检,某市环卫局准备购买A、B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元;购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.(1)、每个A型垃圾箱和B型垃圾箱各多少元?(2)、现需要购买A,B两种型号的垃圾箱共300个,分别由甲、乙两人进行安装,要求在12天内完成(两人同时进行安装).已知甲负责A型垃圾箱的安装,每天可以安装15个,乙负责B型垃圾箱的安装,每天可以安装20个,生产厂家表示若购买A型垃圾箱不少于150个时,该型号的产品可以打九折;若购买B型垃圾箱超过150个时,该型号的产品可以打八折,若既能在规定时间内完成任务,费用又最低,应购买A型和B型垃圾箱各多少个?最低费用是多少元?22.
某体育场看台的坡面AB与地面的夹角是37°,看台最高点B到地面的垂直距离BC为3.6米,看台正前方有一垂直于地面的旗杆DE,在B点用测角仪测得旗杆的最高点E的仰角为33°,已知测角仪BF的高度为1.6米,看台最低点A与旗杆底端D之间的距离为16米(C,A,D在同一条直线上).
 (1)、求看台最低点A到最高点B的坡面距离;(2)、一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)
(1)、求看台最低点A到最高点B的坡面距离;(2)、一面红旗挂在旗杆上,固定红旗的上下两个挂钩G、H之间的距离为1.2米,下端挂钩H与地面的距离为1米,要求用30秒的时间将红旗升到旗杆的顶端,求红旗升起的平均速度(计算结果保留两位小数)(sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin33°≈0.54,cos33°≈0.84,tan33°≈0.65)六、解答题
-
23. 如图,在⊙O中,直径AB垂直弦CD于E,过点A作∠DAF=∠DAB,过点D作AF的垂线,垂足为F,交AB的延长线于点P,连接CO并延长交⊙O于点G,连接EG,已知DE=4,AE=8.
 (1)、求证:DF是⊙O的切线;(2)、求证:OC2=OE•OP;(3)、求线段EG的长.24.
(1)、求证:DF是⊙O的切线;(2)、求证:OC2=OE•OP;(3)、求线段EG的长.24.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
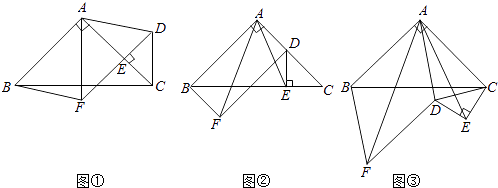 (1)、请直接写出线段AF,AE的数量关系;(2)、将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)、在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
(1)、请直接写出线段AF,AE的数量关系;(2)、将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)、在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.七、解答题
-
25.
如图,在平面直角坐标系中,抛物线y=ax2+ x+c(a≠0)与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线x= .
 (1)、求抛物线的解析式;(2)、M为第一象限内的抛物线上的一个点,过点M作MG⊥x轴于点G,交AC于点H,当线段CM=CH时,求点M的坐标;(3)、在(2)的条件下,将线段MG绕点G顺时针旋转一个角α(0°<α<90°),在旋转过程中,设线段MG与抛物线交于点N,在线段GA上是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.
(1)、求抛物线的解析式;(2)、M为第一象限内的抛物线上的一个点,过点M作MG⊥x轴于点G,交AC于点H,当线段CM=CH时,求点M的坐标;(3)、在(2)的条件下,将线段MG绕点G顺时针旋转一个角α(0°<α<90°),在旋转过程中,设线段MG与抛物线交于点N,在线段GA上是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.