2017年山东省淄博市沂源县中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题：

1. 观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 小军将一个直角三角板（如图）绕它的一条直角边所在的直线旋转一周形成一个几何体，将这个几何体的侧面展开得到的大致图形是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、2 $\sqrt{3}$ +3 $\sqrt{3}$ =5 $\sqrt{6}$ B、（ $\sqrt{2} + 1$ ）（1﹣ $\sqrt{2}$ ）=1 C、（xy）^﹣¹（ $\frac{1}{2}$ xy）²= $\frac{1}{4}$ xy D、﹣（﹣a）⁴÷a²=a²

查看试题解析
4. 如图，一束光线与水平面成60°的角度照射地面，现在地面AB上支放一个平面镜CD，使这束光线经过平面镜反射后成水平光线，则平面镜CD与地面AB所成角∠DCB的度数等于（）

A、30° B、45° C、50° D、60°

查看试题解析
5. 甲、乙两人5次射击命中的环数如下：
甲
7
9
8
6
10
乙
7
8
9
8
8
则以下判断中正确的是（）

A、 $\bar{x}$ _甲= $\bar{x}$ _乙， S_甲²=S_乙² ． B、 $\bar{x}$ _甲= $\bar{x}$ _乙， S_甲²＞S_乙² ． C、 $\bar{x}$ _甲= $\bar{x}$ _乙， S_甲²＜S_乙² ． D、 $\bar{x}$ _甲＜ $\bar{x}$ _乙， S_甲²＜S_乙² ．

查看试题解析
6. 一只盒子中有红球m个，白球8个，黑球n个，每个球除颜色外都相同，从中任取一个球，取得是白球的概率与不是白球的概率相同，那么m与n的关系是（　　）

A、m+n=8 B、m+n=4 C、m=n=4 D、m=3，n=5

查看试题解析
7. 在如图4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M₁N₁P₁ ，则其旋转中心可能是（）

A、点A B、点B C、点C D、点D

查看试题解析
8. 用计算器计算时，下列说法错误的是（）

A、计算“ $\frac{1}{2}$ ﹣1 $\frac{3}{4}$ ”的按键顺序是 B、计算“3×10⁵﹣28”的按键顺序是 C、“已知SinA=0.3，求锐角A”的按键顺序是 D、计算“（ $\frac{1}{2}$ ）⁵”的按键顺序是

查看试题解析
9. 如图，AB是⊙的直径，弦CD垂直平分OB，则∠BDC=（）

A、15° B、20° C、30° D、45°

查看试题解析
10. 已知一列数：1，﹣2，3，﹣4，5，﹣6，7，…将这列数排成下列形式：
第1行   1
第2行﹣2   3
第3行﹣4   5﹣6
第4行 7﹣8　9﹣10
第5行 11﹣12 13﹣14 15
…
按照上述规律排下去，那么第100行从左边数第5个数是（   ）

A、﹣4955 B、4955 C、﹣4950 D、4950

查看试题解析
11.
函数y= $\frac{4}{x}$ 和y= $\frac{1}{x}$ 在第一象限内的图象如图，点P是y= $\frac{4}{x}$ 的图象上一动点，PC⊥x轴于点C，交y= $\frac{1}{x}$ 的图象于点B．给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA= $\frac{1}{3}$ AP．其中所有正确结论的序号是（　　）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析
12. 如图，在矩形ABCD中，BC=8，AB=6，经过点B和点D的两个动圆均与AC相切，且与AB、BC、AD、DC分别交于点G、H、E、F，则EF+GH的最小值是（）

A、6 B、8 C、9.6 D、10

查看试题解析

二、填空题：

13. 因式分解（a+b）（a+b﹣1）﹣a﹣b+1的结果为．

查看试题解析
14. 已知a²﹣a﹣2=0，则代数式 $\frac{1}{a}$ ﹣ $\frac{1}{a - 1}$ 的值为．

查看试题解析
15. 如图，已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点．若△ABC与△A₁B₁C₁是位似图形，且顶点都在格点上，则位似中心的坐标是．

查看试题解析
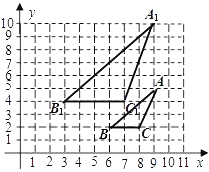16. 如图，三角板ABC的两直角边AC，BC的长分别是40cm和30cm，点G在斜边AB上，且BG=30cm，将这个三角板以G为中心按逆时针旋转90°，至△A′B′C′的位置，那么旋转后两个三角板重叠部分（四边形EFGD）的面积为 cm² ．

查看试题解析
17. 如图，在以AB为直径的半圆中，有一个边长为1的内接正方形CDEF，则以AC和BC的长为两根的一元二次方程是．

查看试题解析

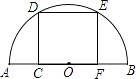
三、解答题：

18. 如图，直线a∥b，Rt△ABC的顶点B在直线a上，∠C=90°，∠β=55°，求∠α的度数．

查看试题解析
19.
某校对九年级学生进行了一次数学学业水平测试，成绩评定分为A、B、C、D四个等级（注：等级A、B、C、D分别代表优秀、良好、合格、不合格），学校从九年级学生中随机抽取50名学生的数学成绩进行统计分析，并绘制成扇形统计图（如图所示）．
根据图中所给的信息答下列问题：

(1)、随机抽取的九年级学生数学学业水平测试中，D等级人数的百分率和D等级学生人数分别是多少？

(2)、这次随机抽样中，学生数学学业水平测试成绩的中位数落在哪个等级？

(3)、若该校九年级学生有800名，请你估计这次数学学业水平测试中，成绩达合格以上（含合格）的人数大约有多少人？

查看试题解析
20. 已知：如图，在△ABC中，AB=AC，AD是BC边上的中线，AE∥BC，CE⊥AE，垂足为E．

(1)、求证：△ABD≌△CAE；

(2)、连接DE，线段DE与AB之间有怎样的位置和数量关系？请证明你的结论．

查看试题解析
21. 一元二次方程x²﹣2x﹣ $\frac{5}{4}$ =0的某个根，也是一元二次方程x²﹣（k+2）x+ $\frac{9}{4}$ =0的根，求k的值．

查看试题解析
22. 如图，小明在研究性学习活动中，对自己家所在的小区进行调查后发现，小区汽车入口宽AB为3.2m，在入口的一侧安装了停止杆CD，其中AE为支架．当停止杆仰起并与地面成60°角时，停止杆的端点C恰好与地面接触．此时CA为0.7m．在此状态下，若一辆货车高3m，宽2.5m，入口两侧不能通车，那么这辆货车在不碰杆的情况下，能从入口内通过吗？请你通过估算说明．（参考数据： $\sqrt{3}$ ≈1.7）

查看试题解析
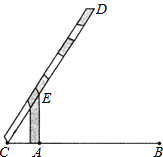23. 已知抛物线y=ax²+bx+c的顶点为（1，0），且经过点（0，1）．

(1)、求该抛物线对应的函数的解析式；

(2)、将该抛物线向下平移m（m＞0）个单位，设得到的抛物线的顶点为A，与x轴的两个交点为B、C，若△ABC为等边三角形．
①求m的值；
②设点A关于x轴的对称点为点D，在抛物线上是否存在点P，使四边形CBDP为菱形？若存在，写出点P的坐标；若不存在，请说明理由．

查看试题解析
24.
在Rt△ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP= $\frac{12}{13}$ ．

(1)、如图1，当点E与点C重合时，求CM的长；

(2)、
如图2，当点E在边AC上时，点E不与点A，C重合，设AP=x，BN=y，求y关于x的函数关系式，并写出x的取值范围；

(3)、若△AME∽△ENB，求AP的长．

查看试题解析

甲	7	9	8	6	10
乙	7	8	9	8	8