2017年山东省淄博市沂源县中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 在实数0,﹣ , ,|﹣2|中,最小的是( )A、 B、﹣ C、0 D、|﹣2|2. 下面四个图形中,能判断∠1>∠2的是( )A、
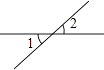 B、
B、 C、
C、 D、
D、 3. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
3. 如图,在平面直角坐标系中,点B,C,E,在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )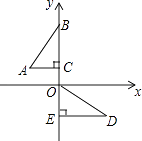 A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移34. 已知实数x、y同时满足三个条件:①3x﹣2y=4﹣p,②4x﹣3y=2+p,③x>y,那么实数p的取值范围是( )A、p>﹣1 B、p<1 C、p<﹣1 D、p>15. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A、△ABC绕点C顺时针旋转90°,再向下平移3 B、△ABC绕点C顺时针旋转90°,再向下平移1 C、△ABC绕点C逆时针旋转90°,再向下平移1 D、△ABC绕点C逆时针旋转90°,再向下平移34. 已知实数x、y同时满足三个条件:①3x﹣2y=4﹣p,②4x﹣3y=2+p,③x>y,那么实数p的取值范围是( )A、p>﹣1 B、p<1 C、p<﹣1 D、p>15. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )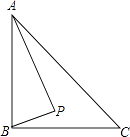 A、 B、2 C、 D、6. 如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
A、 B、2 C、 D、6. 如图,边长为(m+3)的正方形纸片,剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )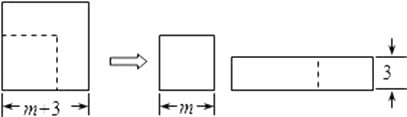 A、m+3 B、m+6 C、2m+3 D、2m+67. 给出下列四个命题:
A、m+3 B、m+6 C、2m+3 D、2m+67. 给出下列四个命题:①如果某圆锥的侧面展开图是半圆,则其轴截面一定是等边三角形;
②若点A在直线y=2x﹣3上,且点A到两坐标轴的距离相等,则点A在第一或第四象限;
③半径为5的圆中,弦AB=8,则圆周上到直线AB的距离为2的点共有四个;
④若A(a,m)、B(a﹣1,n)(a>0)在反比例函y= 的图象上,则m<n.
其中,正确命题的个数是( )
A、1个 B、2个 C、3个 D、4个8. 关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足( )A、a≥1 B、a>1且a≠5 C、a≥1且a≠5 D、a≠59. 如图,是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )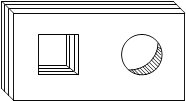 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
10. 如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( ) A、 B、 C、 D、11. 如图,已知点A是直线y=x与反比例函数y= (k>0,x>0)的交点,B是y= 图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A、 B、 C、 D、11. 如图,已知点A是直线y=x与反比例函数y= (k>0,x>0)的交点,B是y= 图象上的另一点,BC//x轴,交y轴于点C.动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设四边形OMPN的面积为S,P点运动时间为t,则S关于t的函数图象大致为( ) A、
A、 B、
B、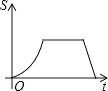 C、
C、 D、
D、 12. 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )
12. 如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )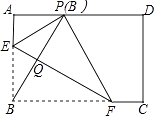 A、①② B、②③ C、①③ D、①④
A、①② B、②③ C、①③ D、①④二、填空题
-
13. 据某市统计网消息,在全国第六次人口普查中显示,该市常住人口总数约为5400000人,将这个总人口数用科学记数法表示为 .14. 一组数据:1,3,2,3,1,0,2的中位数是 .15. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应的读数是度.
 16. 在△ABC中,AB=12 ,AC=13,cos∠B= ,则BC边长为 .17. 若函数y=mx2﹣6x+1(m是常数)的图象与x轴只有一个交点,m的值为 .
16. 在△ABC中,AB=12 ,AC=13,cos∠B= ,则BC边长为 .17. 若函数y=mx2﹣6x+1(m是常数)的图象与x轴只有一个交点,m的值为 .三、解答题
-
18. 计算: ﹣2× +( )﹣1+(π﹣2017)0 .19. 尺规作图:如图,已知△ABC.
求作△A1B1C1 , 使A1B1=AB,∠B1=∠B,B1C1=BC.
(作图要求:写已知、求作,不写作法,不证明,保留作图痕迹)
已知:
求作:
 20. 在一个不透明的盒子里,装有三个分别写有数字﹣1,0,1的乒乓球(形状,大小一样),先从盒子里随即取出一个乒乓球,记下数字后放回盒子,摇匀后再随即取出一个乒乓球,记下数字.(1)、请用树状图或列表的方法求两次取出乒乓球上数字相同的概率;(2)、求两次取出乒乓球上数字之积等于0的概率.21. 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F.
20. 在一个不透明的盒子里,装有三个分别写有数字﹣1,0,1的乒乓球(形状,大小一样),先从盒子里随即取出一个乒乓球,记下数字后放回盒子,摇匀后再随即取出一个乒乓球,记下数字.(1)、请用树状图或列表的方法求两次取出乒乓球上数字相同的概率;(2)、求两次取出乒乓球上数字之积等于0的概率.21. 如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连接CC′交斜边于点E,CC′的延长线交BB′于点F. (1)、证明:△ACE∽△FBE;(2)、设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.22. 华昌中学开学初在金利源商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.(1)、求购买一个A品牌、一个B品牌的足球各需多少元?(2)、华昌中学响应习总书记“足球进校园”的号召,决定两次购进A、B两种品牌足球共50个,恰逢金利源商场对两种品牌足球的售价进行调整,A品牌足球售价比第一次购买时提高了8%,B品牌足球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌足球的总费用不超过3260元,那么华昌中学此次最多可购买多少个B品牌足球?23. 在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
(1)、证明:△ACE∽△FBE;(2)、设∠ABC=α,∠CAC′=β,试探索α、β满足什么关系时,△ACE与△FBE是全等三角形,并说明理由.22. 华昌中学开学初在金利源商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.(1)、求购买一个A品牌、一个B品牌的足球各需多少元?(2)、华昌中学响应习总书记“足球进校园”的号召,决定两次购进A、B两种品牌足球共50个,恰逢金利源商场对两种品牌足球的售价进行调整,A品牌足球售价比第一次购买时提高了8%,B品牌足球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌足球的总费用不超过3260元,那么华昌中学此次最多可购买多少个B品牌足球?23. 在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:第一步:对折矩形纸片ABCD,使AD与BC重合,把纸片展开,得到折痕EF(如图1);
第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).

请解答以下问题:
(1)、如图2,若延长MN交BC于P,△BMP是什么三角形?请证明你的结论;(2)、在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP?(3)、设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系.设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点),为什么?24. 解答题(1)、问题:如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:AD•BC=AP•BP; (2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(2)、探究:如图2,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由. (3)、应用:请利用(1)(2)获得的经验解决问题:
(3)、应用:请利用(1)(2)获得的经验解决问题:如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A,设点P的运动时间为t(秒),当DC=4BC时,求t的值.
