2017年山东省淄博市博山区中考数学一模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题：

1. 下列关系式正确的是（）

A、35.5°=35°5′ B、35.5°=35°50′ C、35.5°＜35°5′ D、35.5°＞35°5′

查看试题解析
2. 运用乘法公式计算（x+3）²的结果是（）

A、x²+9 B、x²﹣6x+9 C、x²+6x+9 D、x²+3x+9

查看试题解析
3. 到三角形三个顶点的距离都相等的点是这个三角形的（）

A、三条高的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条边的垂直平分线的交点

查看试题解析
4. 下列分式中，最简分式是（）

A、 $\frac{x^{2} - 1}{x^{2} + 1}$ B、 $\frac{x + 1}{x^{2} - 1}$ C、 $\frac{x^{2} - 2 x y + y^{2}}{x^{2} - x y}$ D、 $\frac{x^{2} - 36}{2 x + 12}$

查看试题解析
5. 把多项式x²+ax+b分解因式，得（x+1）（x﹣3）则a，b的值分别是（）

A、a=2，b=3 B、a=﹣2，b=﹣3 C、a=﹣2，b=3 D、a=2，b=﹣3

查看试题解析
6. 下列计算正确的是（）

A、 $\sqrt{12}$ =2 $\sqrt{3}$ B、 $\sqrt{\frac{3}{2}}$ = $\frac{\sqrt{3}}{2}$ C、 $\sqrt{- x^{3}}$ =x $\sqrt{- x}$ D、 $\sqrt{x^{2}}$ =x

查看试题解析
7. 点A，B在数轴上的位置如图所示，其对应的数分别是a和b．对于以下结论：
甲：b﹣a＜0
乙：a+b＞0
丙：|a|＜|b|
丁： $\frac{b}{a}$ ＞0
其中正确的是（）

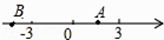A、甲乙 B、丙丁 C、甲丙 D、乙丁

查看试题解析
8. 已知关于x，y的方程x^2m^﹣n﹣2+4y^m+n+1=6是二元一次方程，则m，n的值为（）

A、m=1，n=﹣1 B、m=﹣1，n=1 C、 $m = \frac{1}{3} ， n = - \frac{4}{3}$ D、 $m = - \frac{1}{3} ， n = \frac{4}{3}$

查看试题解析
9. 如图，矩形ABCD的顶点A、C分别在直线a、b上，且a//b，∠1=60°，则∠2的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
10. 如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是（0，a），（﹣3，2），（b，m），（c，m），则点E的坐标是（）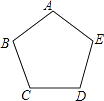

A、（2，﹣3） B、（2，3） C、（3，2） D、（3，﹣2）

查看试题解析
11.
如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）

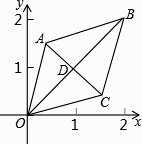A、（1，﹣1） B、（﹣1，﹣1） C、（ $\sqrt{2}$ ，0） D、（0，﹣ $\sqrt{2}$ ）

查看试题解析

二、填空题：

12. 若代数式x+2的值为1，则x等于．

查看试题解析
13. 如图，直线y=x+b与直线y=kx+6交于点P（3，5），则关于x的不等式x+b＞kx+6的解集是．

查看试题解析
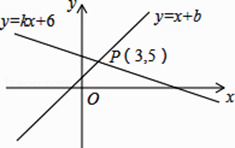14. 某几何体的三视图如图所示，则组成该几何体的小正方体的个数是．

查看试题解析
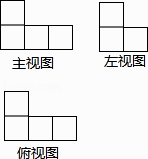15. 如图是一张长方形纸片ABCD，已知AB=8，AD=7，E为AB上一点，AE=5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．

查看试题解析
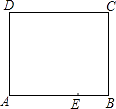16. 如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，能完全覆盖这个平面图形的圆面的最小半径是 mm．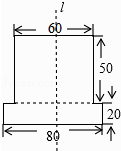

查看试题解析

三、解答题：

17. 如图，▱ABCD对角线AC、BD相交于点O，E，F分别是OA，OC的中点，连接BE，DF．

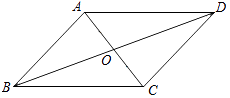(1)、根据题意，补全图形；

(2)、求证：BE=DF．

查看试题解析
18. 已知关于x的一元二次方程x²﹣6x+（2m+1）=0有实数根．

(1)、求m的取值范围；

(2)、如果方程的两个实数根为x₁ ， x₂ ，且2x₁x₂+x₁+x₂≥20，求m的取值范围．

查看试题解析
19.
如图，在平面直角坐标系中，反比例函数y= $\frac{k}{x}$ （x＞0）的图象上有一点A（m，4），过点A作AB⊥x轴于点B，将点B向右平移2个单位长度得到点C，过点C作y轴的平行线交反比例函数的图象于点D，CD= $\frac{4}{3}$

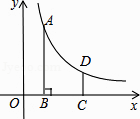(1)、点D的横坐标为（用含m的式子表示）；

(2)、求反比例函数的解析式．

查看试题解析
20. 在一次社会调查活动中，小华收集到某“健步走运动”团队中20名成员一天行走的步数，记录如下：
5640   6430    6520 6798 7325
8430   8215    7453 7446 6754
7638   6834    7326 6830 8648
8753   9450    9865 7290 7850
对这20个数据按组距1000进行分组，并统计整理，绘制了如下尚不完整的统计图表：
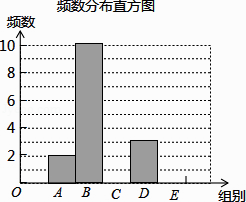
步数分组统计表
组别
步数分组
频数
A
5500≤x＜6500
2
B
6500≤x＜7500
10
C
7500≤x＜8500
m
D
8500≤x＜9500
3
E
9500≤x＜10500
n
请根据以上信息解答下列问题：

(1)、求m，n的值；

(2)、补全频数发布直方图；

(3)、这20名“健步走运动”团队成员一天行走步数的中位数落在哪一组？

(4)、若该团队共有120人，请估计其中一天行走步数不少于7500步的人数．

查看试题解析
21.
如图，在大楼AB的正前方有一斜坡CD，CD=4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．

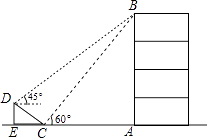(1)、求斜坡CD的高度DE；

(2)、求大楼AB的高度（结果保留根号）

查看试题解析
22. 如图，半圆O的直径AB=4，以长为2的弦PQ为直径，向点O方向作半圆M，其中P点在 $\hat{A Q}$ 上且不与A点重合，但Q点可与B点重合．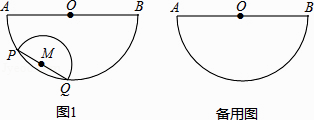

发现： $\hat{A P}$ 的长与 $\hat{Q B}$ 的长之和为定值l，求l：

查看试题解析
23. 设抛物线的解析式为y=ax² ，过点B₁（1，0）作x轴的垂线，交抛物线于点A₁（1，2）；过点B₂（ $\frac{1}{2}$ ，0）作x轴的垂线，交抛物线于点A₂；…；过点B_n（（ $\frac{1}{2}$ ）^n﹣1 ， 0）（n为正整数）作x轴的垂线，交抛物线于点A_n ，连接A_nB_n+1 ，得Rt△A_nB_nB_n+1 ．

(1)、求a的值；

(2)、直接写出线段A_nB_n ， B_nB_n+1的长（用含n的式子表示）；

(3)、在系列Rt△A_nB_nB_n+1中，探究下列问题：
①当n为何值时，Rt△A_nB_nB_n+1是等腰直角三角形？
②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△A_kB_kB_k+1与Rt△A_mB_mB_m+1相似？若存在，求出其相似比；若不存在，说明理由．

查看试题解析

组别	步数分组	频数
A	5500≤x＜6500	2
B	6500≤x＜7500	10
C	7500≤x＜8500	m
D	8500≤x＜9500	3
E	9500≤x＜10500	n