2017年山东省枣庄市峄城区中考数学三模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题:
-
1. 在(﹣1)2017 , (﹣3)0 , ,( )﹣2 , 这四个数中,最大的数是( )A、(﹣1)2017 B、(﹣3)0 C、 D、( )﹣22. 下列运算正确的是( )A、+ = B、3x2y﹣x2y=3 C、 =a+b D、(a2b)3=a6b33. 若关于x的方程x2+2x+a=0不存在实数根,则a的取值范围是( ).A、a<1 B、a>1 C、a≤1 D、a≥14. 若某几何体的三视图如图所示,则该几何体是( )
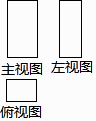 A、
A、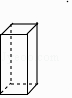 B、
B、 C、
C、 D、
D、 5. 某市6月上旬前5天的最高气温如下(单位:℃):28,29,31,29,32.对这组数据,下列说法正确的是( )A、平均数为30 B、众数为29 C、中位数为31 D、极差为56. 周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( )
5. 某市6月上旬前5天的最高气温如下(单位:℃):28,29,31,29,32.对这组数据,下列说法正确的是( )A、平均数为30 B、众数为29 C、中位数为31 D、极差为56. 周末小石去博物馆参加综合实践活动,乘坐公共汽车0.5小时后想换乘另一辆公共汽车,他等候一段时间后改为利用手机扫码骑行摩拜单车前往.已知小石离家的路程s(单位:千米)与时间t(单位:小时)的函数关系的图象大致如图.则小石骑行摩拜单车的平均速度为( ) A、30千米/小时 B、18千米/小时 C、15千米/小时 D、9千米/小时7. 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA , 则△ABC与△DEF的面积之比为( )
A、30千米/小时 B、18千米/小时 C、15千米/小时 D、9千米/小时7. 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA , 则△ABC与△DEF的面积之比为( )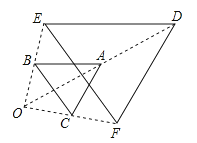 A、1:2 B、1:4 C、1:5 D、1:68. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( )
A、1:2 B、1:4 C、1:5 D、1:68. 如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( ) A、 B、 C、 D、9. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A、 B、 C、 D、9. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )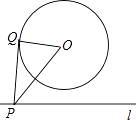 A、 B、 C、3 D、210. 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( )
A、 B、 C、3 D、210. 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=2,FD=4,则BC的长为( ) A、6 B、2 C、4 D、411. 如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2 , 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 下列判断:
A、6 B、2 C、4 D、411. 如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2 , 若y1≠y2 , 取y1、y2中的较小值记为M;若y1=y2 , 记M=y1=y2 . 下列判断:①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x=1.
其中正确的有( )
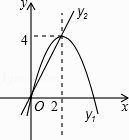 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题:
-
12. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为 .13. 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是 .
 14. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为 .
14. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为 . 15. 如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为(结果保留π).
15. 如图,△ABC是边长为4的等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为(结果保留π). 16.
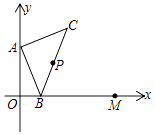
16.如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为 .
 17. 如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= .
17. 如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= .
三、解答题:
-
18. 先化简,再求代数式 的值,其中a=3tan30°+1,b= cos45°.19. 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40

请根据所给信息,解答下列问题:
(1)、a= , b= , 且补全频数分布直方图;(2)、若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?(3)、在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.20. 如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线y= (m≠0)交于点A(2,﹣3)和点B(n,2). (1)、求直线与双曲线的表达式;(2)、对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.21. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)、求直线与双曲线的表达式;(2)、对于横、纵坐标都是整数的点给出名称叫整点.动点P是双曲线y= (m≠0)上的整点,过点P作垂直于x轴的直线,交直线AB于点Q,当点P位于点Q下方时,请直接写出整点P的坐标.21. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E. (1)、求证:DC=DE;(2)、若tan∠CAB= ,AB=3,求BD的长.22. 浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
(1)、求证:DC=DE;(2)、若tan∠CAB= ,AB=3,求BD的长.22. 浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:销售时段
销售数量
销售收入
A种型号
B种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)、求A、B两种型号的电风扇的销售单价;(2)、若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?(3)、在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.23. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. (1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.24.
(1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.24.如图,已知抛物线y=ax2+bx+c经过A(﹣2,0),B(4,0),C(0,3)三点.
 (1)、求该抛物线的解析式;(2)、在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;(3)、若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.
(1)、求该抛物线的解析式;(2)、在y轴上是否存在点M,使△ACM为等腰三角形?若存在,请直接写出所有满足要求的点M的坐标;若不存在,请说明理由;(3)、若点P(t,0)为线段AB上一动点(不与A,B重合),过P作y轴的平行线,记该直线右侧与△ABC围成的图形面积为S,试确定S与t的函数关系式.