2017年山东省临沂市中考数学模拟试卷(一)
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣ 的相反数是( )A、2 B、﹣2 C、﹣ D、2. 一个两边平行的纸条,如图那样折叠一下,则∠1的度数是( )
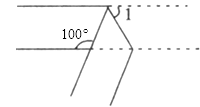 A、30° B、40° C、50° D、60°3. 下列各式计算正确的是( )A、a2+a2=a4 B、(﹣2x)3=﹣8x3 C、a3•a4=a12 D、(x﹣3)2=x2﹣94. 下面四个手机应用图标中是轴对称图形的是( )A、
A、30° B、40° C、50° D、60°3. 下列各式计算正确的是( )A、a2+a2=a4 B、(﹣2x)3=﹣8x3 C、a3•a4=a12 D、(x﹣3)2=x2﹣94. 下面四个手机应用图标中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 某校九年级一班学生参加体育考试,第一小组学生引体向上的成绩如表所示:
5. 某校九年级一班学生参加体育考试,第一小组学生引体向上的成绩如表所示:引体向上的个数
7
8
9
10
人数
2
1
4
5
则这组学生引体向上个数的众数和中位数分别为( )
A、10和9 B、9和10 C、10和9.5 D、9.5和106. 不等式组 的整数解有( )A、3个 B、4个 C、5个 D、6个7. 在一张边长为4cm的正方形纸上做扎针随机试验,纸上有一个半径为1cm的圆形阴影区域,则针头扎在阴影区域内的概率为( )A、 B、 C、 D、8. 当x=3时,分式( ﹣x﹣1)÷ 的值为( )A、 B、 C、 D、9. 如图,△ABC内接于⊙O,AC是⊙O的直径,∠ACB=40°,点D是弧BAC上一点,连结CD.则∠D的度数是( ) A、50° B、45° C、40° D、35°10.
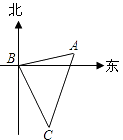
A、50° B、45° C、40° D、35°10.如图,客轮在海上以30km/h的速度由B向C航行,在B处测得灯塔A的方向角为北偏东80°,测得C处的方向角为南偏东25°,航行1小时后到达C处,在C处测得A的方向角为北偏东20°,则C到A的距离是( )
 A、15 km B、15 km C、15( + )km D、5( +3 )km11. 如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
A、15 km B、15 km C、15( + )km D、5( +3 )km11. 如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )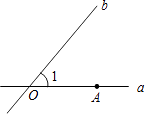 A、1个 B、2个 C、3个 D、4个12.
A、1个 B、2个 C、3个 D、4个12.如图,已知动点P在函数y= (x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AF•BE的值为( )
 A、4 B、2 C、1 D、13.
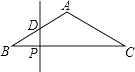
A、4 B、2 C、1 D、13.如图,已知△ABC中,AB=AC=2,∠B=30°,P是BC边上一个动点,过点P作PD⊥BC,交△ABC的AB边于点D.若设PD为x,△BPD的面积为y,则y与x之间的函数关系的图象大致是( )
 A、
A、 B、
B、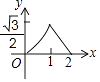 C、
C、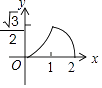 D、
D、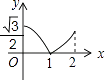
二、填空题
-
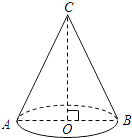
14. 因式分解:3x2y﹣27y= .15. 某药品原价是95元,经连续两次降价后,价格变为60.8元,如果每次降价的百分率是一样的,那么每次降价的百分率是 .16. 在综合实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=6cm,高OC=8cm.则这个圆锥漏斗的侧面积是 .
 17. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为 .
17. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为 .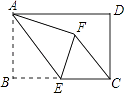 18. 已知,如图,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 周长记作C1;再作第二个正方形A2B2C2A3 , 周长记作C2;继续作第三个正方形A3B3C3A4 , 周长记作C3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Cn= .
18. 已知,如图,∠MON=45°,OA1=1,作正方形A1B1C1A2 , 周长记作C1;再作第二个正方形A2B2C2A3 , 周长记作C2;继续作第三个正方形A3B3C3A4 , 周长记作C3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第n个正方形的周长Cn= .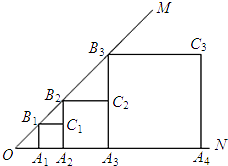
三、三.解答题
-
19. 计算:﹣32+6cos45°﹣ (2﹣ )+| ﹣3|.20. 为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:
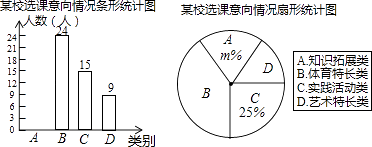 (1)、求扇形统计图中m的值,并补全条形统计图;(2)、在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?(3)、已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?21. 如图,已知点E,F分别是▱ABCD的边BC,AD上的中点,且∠BAC=90°.
(1)、求扇形统计图中m的值,并补全条形统计图;(2)、在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?(3)、已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?21. 如图,已知点E,F分别是▱ABCD的边BC,AD上的中点,且∠BAC=90°.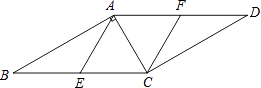 (1)、求证:四边形AECF是菱形;(2)、若∠B=30°,BC=10,求菱形AECF面积.22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N.
(1)、求证:四边形AECF是菱形;(2)、若∠B=30°,BC=10,求菱形AECF面积.22. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点M,MN⊥AC于点N.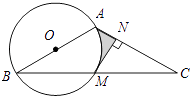 (1)、求证:MN是⊙O的切线;(2)、若∠BAC=120°,AB=2,求图中阴影部分的面积.23. 光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
(1)、求证:MN是⊙O的切线;(2)、若∠BAC=120°,AB=2,求图中阴影部分的面积.23. 光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800
1600
B地区
1600
1200
(1)、设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;(2)、若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;(3)、如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.24.如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
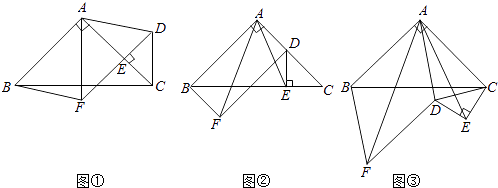 (1)、请直接写出线段AF,AE的数量关系;(2)、将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)、在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.25.
(1)、请直接写出线段AF,AE的数量关系;(2)、将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;(3)、在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.25.如图,抛物线y=﹣ x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
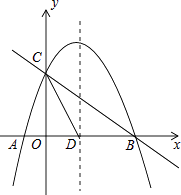 (1)、求抛物线的表达式;(2)、在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
(1)、求抛物线的表达式;(2)、在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.