2017年山东省泰安市肥城市中考数学二模试卷

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、选择题

1. |﹣2017|的相反数是（）

A、2017 B、 $\frac{1}{2017}$ C、﹣2017 D、﹣ $\frac{1}{2017}$

查看试题解析
2. 下列运算正确的是（）

A、2a+3b=5ab B、a²•a³=a⁵ C、（2a）³=6a ³ D、a⁶+a³=a⁹

查看试题解析
3.
一个几何体及它的主视图和俯视图如图所示，那么它的左视图正确的是（）

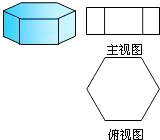A、 B、 C、 D、

查看试题解析
4. 据国家统计局公布，2015年我国国内生产总值约为676700亿元（人民币），用科学记数法表示数据“676700亿”，结果是（）

A、6.767×10⁵ B、6.767×10¹² C、6.767×10¹³ D、6.767×10¹⁴

查看试题解析
5. 以下图形中对称轴的数量小于3的是（　　）

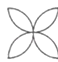A、 B、 C、 D、

查看试题解析
6. 化简（ $\frac{x}{x - 1}$ ﹣ $\frac{2 x + 2}{x^{2} - 1}$ ） $\div \frac{x - 2}{x^{2} - x}$ 的结果是（）

A、x B、 $\frac{1}{x}$ C、 $\frac{x + 1}{x - 1}$ D、 $\frac{x - 1}{x + 1}$

查看试题解析
7. 如图，将矩形纸片ABCD中折叠，使顶点B落在边AD的E点上折痕FG交BC于G，交AB于F，若∠AEF=20°，则∠FGB的度数为（）

A、25° B、30° C、35° D、40°

查看试题解析
8. 某单位若干名职工参加普法知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图，根据图中提供的信息，这些职工成绩的中位数和平均数分别是（）

A、94分，96分 B、96分，96分 C、94分，96.4分 D、96分，96.4分

查看试题解析
9. 甲仓库乙仓库共存粮450吨，现从甲仓库运出存粮的60%，从乙仓库运出存粮的40%．结果乙仓库所余的粮食比甲仓库所余的粮食多30吨．若设甲仓库原来存粮x吨，乙仓库原来存粮y吨，则有（）

A、 ${\begin{matrix} x + y = 450 \\ (1 - 60 %) x - (1 - 40 %) y = 30 \end{matrix}$ B、 ${\begin{matrix} x + y = 450 \\ 60 % x - 40 % y = 30 \end{matrix}$ C、 ${\begin{matrix} x + y = 450 \\ (1 - 40 %) y - (1 - 60 %) x = 30 \end{matrix}$ D、 ${\begin{matrix} x + y = 450 \\ 40 % y - 60 % x = 30 \end{matrix}$

查看试题解析
10. 将某抛物线图象向右平移2个单位，再向下平移3个单位所得的抛物线是y=﹣2x²+4x+1的图象，则将该抛物线沿y轴翻折后所得的函数关系式是（）

A、y=﹣2（x﹣1）²+6 B、y=﹣2（x﹣1）²﹣6 C、y=﹣2（x+1）²+6 D、y=2（x+1）²﹣6

查看试题解析
11. 如图，在等边△ABC中，点O在边AB上，⊙O过点B且分别与边AB、BC相交于点D、E、F是AC上的点，判断下列说法错误的是（）

A、若EF⊥AC，则EF是⊙O的切线 B、若EF是⊙O的切线，则EF⊥AC C、若BE=EC，则AC是⊙O的切线 D、若BE= $\frac{\sqrt{3}}{2}$ EC，则AC是⊙O的切线

查看试题解析
12. 若关于x的一元二次方程kx²﹣（2k+1）x+k+2=0，有两个不相等的实数根，则k的取值范围是（）

A、k≤ $\frac{1}{4}$ B、k≤ $\frac{1}{4}$ 且k≠0 C、k＞ $\frac{1}{4}$ D、k＜ $\frac{1}{4}$ 且k≠0

查看试题解析
13. 如图，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=42°，则∠P的度数为（）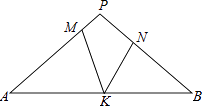

A、44° B、66° C、96° D、92°

查看试题解析
14. 如图，随机闭合开关S₁、S₂、S₃中的两个，则能让灯泡⊗发光的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
15. 如图所示，在扇形BAD中，点C在 $\hat{B D}$ 上，且∠BDC=30°，AB=2 $\sqrt{2}$ ，∠BAD=105°，过点C作CE⊥AD，则图中阴影部分的面积为（）

A、π﹣2 B、π﹣1 C、2π﹣2 D、2π+1

查看试题解析
16. 如果不等式组 $\{\begin{matrix} x > a \\ x < 2 \end{matrix}$ 恰有3个整数解，则a的取值范围是（　　）

A、a≤﹣1 B、a＜﹣1 C、﹣2≤a＜﹣1 D、﹣2＜a≤﹣1

查看试题解析
17.
如图，在▱ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G．若BG=4 $\sqrt{2}$ ，则△CEF的面积是（　　）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、3 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析
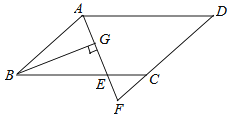18.
如图，菱形ABCD的边AB=8，∠B=60°，P是AB上一点，BP=3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（）

A、5 B、7 C、8 D、 $\frac{13}{2}$

查看试题解析
19. 对于下列结论：
①二次函数y=6x² ，当x＞0时，y随x的增大而增大．
②关于x的方程a（x+m）²+b=0的解是x₁=﹣2，x₂=1（a、m、b均为常数，a≠0），则方程a（x+m+2）²+b=0的解是x₁=﹣4，x₂=﹣1．
③设二次函数y=x²+bx+c，当x≤1时，总有y≥0，当1≤x≤3时，总有y≤0，那么c的取值范围是c≥3．
其中，正确结论的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
20. 如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；② $\frac{A M}{A B} = \frac{A N}{A C}$ ；③△PMN为等边三角形；④当∠ABC=45°时，BN= $\sqrt{2}$ PC．其中正确的个数是（）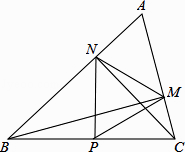

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

21. 分解因式：﹣3x³+12x²﹣12x= ．

查看试题解析
22. 如图，在矩形ABCD中，AB=8，AD=12，过点A、D两点的⊙O与BC边相切于点E，则⊙O的半径为．

查看试题解析
23.
如图，甲、乙两渔船同时从港口O出发外出捕鱼，乙沿南偏东30°方向以每小时10海里的速度航行，甲沿南偏西75°方向以每小时10 $\sqrt{2}$ 海里的速度航行，当航行1小时后，甲在A处发现自己的渔具掉在乙船上，于是迅速改变航向和速度，仍以匀速沿南偏东60°方向追赶乙船，正好在B处追上．则甲船追赶乙船的速度为海里/小时？

查看试题解析
24. 如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A₁处，称为第1次操作，折痕DE到BC的距离记为h₁ ，还原纸片后，再将△ADE沿着过AD中点D₁的直线折叠，使点A落在DE边上的A₂处，称为第2次操作，折痕D₁E₁到BC的距离记为h₂；按上述方法不断操作下去…，经过第2017次操作后得到的折痕D₂₀₁₆E₂₀₁₆ ，到BC的距离记为h₂₀₁₇；若h₁=1，则h₂₀₁₇的值为．

查看试题解析

三、解答题

25. 当前正值樱桃销售季节，小李用20000元在樱桃基地购进樱桃若干进行销售，由于销售状况良好，他又立即拿出60000元资金购进该种樱桃，但这次的进货价比第一次的进货价提高了20%，购进樱桃数量是第一次的2倍还多200千克．

(1)、该种樱桃的第一次进价是每千克多少元？

(2)、如果小李按每千克90元的价格出售，当大部分樱桃售出后，余下500千克按售价的7折出售完，小李销售这种樱桃共盈利多少元．

查看试题解析
26. 如图，正方形AOCB的边长为4，反比例函数y= $\frac{k}{x}$ （k≠0，且k为常数）的图象过点E，且S_△_AOE=3S_△_OBE ．

(1)、求k的值；

(2)、反比例函数图象与线段BC交于点D，直线y= $\frac{1}{2}$ x+b过点D与线段AB交于点F，延长OF交反比例函数y= $\frac{k}{x}$ （x＜0）的图象于点N，求N点坐标．

查看试题解析
27. 如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．

(1)、求证：AD=AF；

(2)、求证：BD=EF；

(3)、试判断四边形ABNE的形状，并说明理由．

查看试题解析
28.
如图，△ABC中，∠ABC=90°，F是AC的中点，过AC上一点D作DE//AB，交BF的延长线于点E，AG⊥BE，垂足是G，连接BD、AE．

(1)、求证：△ABC∽△BGA；

(2)、若AF=5，AB=8，求FG的长；

(3)、当AB=BC，∠DBC=30°时，求 $\frac{D E}{B D}$ 的值．

查看试题解析
29.
如图，已知直线y=kx﹣6与抛物线y=ax²+bx+c相交于A，B两点，且点A（1，﹣4）为抛物线的顶点，点B在x轴上．

(1)、求抛物线的解析式；

(2)、在（1）中抛物线的第二象限图象上是否存在一点P，使△POB与△POC全等？若存在，求出点P的坐标；若不存在，请说明理由；

(3)、若点Q是y轴上一点，且△ABQ为直角三角形，求点Q的坐标．

查看试题解析