2017年山东省临沂市中考数学模拟试卷(三)
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 4的倒数是( )A、4 B、﹣4 C、 D、﹣2. 下列运算正确的是( )A、(a﹣3)2=a2﹣9 B、a2•a4=a8 C、 =±3 D、 =﹣23. 式子 在实数范围内有意义,则x的取值范围是( )A、x≥1 B、x≤1 C、x>0 D、x>14. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁5. 化简: ÷(1﹣ )的结果是( )A、x﹣4 B、x+3 C、 D、6. 如图,EF∥BC,AC平分∠BAF,∠B=80°,∠C=( )度.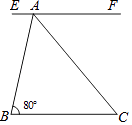 A、40 B、45 C、50 D、557. 如图,已知圆锥侧面展开图的扇形面积为65πcm2 , 扇形的弧长为10πcm,则圆锥母线长是( )
A、40 B、45 C、50 D、557. 如图,已知圆锥侧面展开图的扇形面积为65πcm2 , 扇形的弧长为10πcm,则圆锥母线长是( ) A、5cm B、10cm C、12cm D、13cm8. 如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A、5cm B、10cm C、12cm D、13cm8. 如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( ) A、1.5 B、2.5 C、2.25 D、39. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
A、1.5 B、2.5 C、2.25 D、39. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( ) A、10π B、15π C、20π D、30π10. 已知关于x的二元一次方程组 ,若x+y>3,则m的取值范围是( )A、m>1 B、m<2 C、m>3 D、m>511. 若x=﹣2是关于x的一元二次方程x2+ ax﹣a2=0的一个根,则a的值为( )A、﹣1或4 B、﹣1或﹣4 C、1或﹣4 D、1或412. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )
A、10π B、15π C、20π D、30π10. 已知关于x的二元一次方程组 ,若x+y>3,则m的取值范围是( )A、m>1 B、m<2 C、m>3 D、m>511. 若x=﹣2是关于x的一元二次方程x2+ ax﹣a2=0的一个根,则a的值为( )A、﹣1或4 B、﹣1或﹣4 C、1或﹣4 D、1或412. 如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点.P是直径MN上一动点,则PA+PB的最小值为( )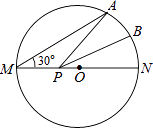 A、 B、1 C、2 D、213. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
A、 B、1 C、2 D、213. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大.
其中正确的结论有( )
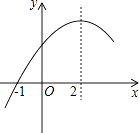 A、1个 B、2个 C、3个 D、4个14. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
A、1个 B、2个 C、3个 D、4个14. 如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )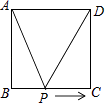 A、
A、 B、
B、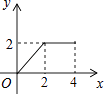 C、
C、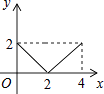 D、
D、
二、填空题
-
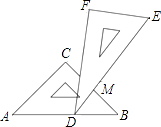
15. 分解因式:ab3﹣4ab= .16. 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度.
 17. “石头、剪刀、布”是广为流传的游戏,游戏时,双方每次任意出“石头”,“剪刀”,“布”这三种手势中的一种,那么双方出现相同手势的概率为 .18. 如图,反比例函数y= (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 .
17. “石头、剪刀、布”是广为流传的游戏,游戏时,双方每次任意出“石头”,“剪刀”,“布”这三种手势中的一种,那么双方出现相同手势的概率为 .18. 如图,反比例函数y= (k>0)的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=2,则k的值为 . 19. 我们把平面内与四边形各边端点构成的三角形都是等腰三角形的点叫做这个四边形的腰点(如矩形的对角线交点是矩形的一个腰点),则正方形的腰点共有个.
19. 我们把平面内与四边形各边端点构成的三角形都是等腰三角形的点叫做这个四边形的腰点(如矩形的对角线交点是矩形的一个腰点),则正方形的腰点共有个.三、解答题
-
20. 计算:( )﹣2﹣6sin30°﹣( )0+ +| ﹣ |21. 为了解学生体育训练的情况,某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试(把成绩结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
 (1)、求本次抽样测试的学生人数;(2)、求扇形图中∠α的度数,并把条形统计图补充完整;(3)、该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人?22. 小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离.
(1)、求本次抽样测试的学生人数;(2)、求扇形图中∠α的度数,并把条形统计图补充完整;(3)、该市九年级共有学生9000名,如果全部参加这次体育测试,则测试等级为D的约有多少人?22. 小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 23. 在等边△ABC中,以BC为直径的⊙O与AB交于点D,DE⊥AC,垂足为点E.
23. 在等边△ABC中,以BC为直径的⊙O与AB交于点D,DE⊥AC,垂足为点E. (1)、求证:DE为⊙O的切线;(2)、计算 .24. 我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元.
(1)、求证:DE为⊙O的切线;(2)、计算 .24. 我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元)
…
70
90
…
销售量y(件)
…
3000
1000
…
(利润=(售价﹣成本价)×销售量)
(1)、求销售量y(件)与售价x(元)之间的函数关系式;(2)、你认为如何定价才能使工艺品厂每天获得的利润为40000元?25. 猜想与证明:如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
 (1)、若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .(2)、如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.
(1)、若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .(2)、如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.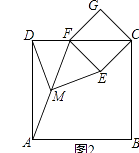 26. 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4﹣x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点.
26. 如图,过A(1,0)、B(3,0)作x轴的垂线,分别交直线y=4﹣x于C、D两点.抛物线y=ax2+bx+c经过O、C、D三点. (1)、求抛物线的表达式;(2)、点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)、若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.
(1)、求抛物线的表达式;(2)、点M为直线OD上的一个动点,过M作x轴的垂线交抛物线于点N,问是否存在这样的点M,使得以A、C、M、N为顶点的四边形为平行四边形?若存在,求此时点M的横坐标;若不存在,请说明理由;(3)、若△AOC沿CD方向平移(点C在线段CD上,且不与点D重合),在平移的过程中△AOC与△OBD重叠部分的面积记为S,试求S的最大值.