广东省广州市广东二师番禺附中2019-2020学年高一上学期数学中考试试卷
试卷更新日期:2019-11-28 类型:期中考试
一、单选题
-
1. 设集合 ,则 =( )A、 B、 C、 D、2. 函数 的定义域为( )A、[ ,3)∪(3,+∞) B、(-∞,3)∪(3,+∞) C、[ ,+∞) D、(3,+∞)3. 下列函数中,既是奇函数又是增函数的为( )A、 B、 C、 D、4. 设函数 = 则 ( )A、 B、 C、1 D、45. , , 的大小关系是( )A、 B、 C、 D、6. 函数 的图象是( )A、
 B、
B、 C、
C、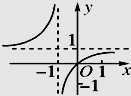 D、
D、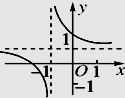 7. 已知函数 在区间 上单调递减,则 取值的集合为( )A、 B、 C、 D、8. 已知函数 ,且 ,则 的值为( )A、-2017 B、-3 C、-1 D、39. 已知 是定义在 上的偶函数,那么 的最大值是( )A、 B、 C、 D、10. 函数 是 上的减函数,则 的取值范围是( )A、(0,1) B、 C、 D、11. 已知偶函数 在区间 上单调递增,则满足 的 的取值范围是( )A、 B、 C、 D、12. 已知 是定义域为 的奇函数,满足 .若 ,则 ( )A、 B、 C、 D、
7. 已知函数 在区间 上单调递减,则 取值的集合为( )A、 B、 C、 D、8. 已知函数 ,且 ,则 的值为( )A、-2017 B、-3 C、-1 D、39. 已知 是定义在 上的偶函数,那么 的最大值是( )A、 B、 C、 D、10. 函数 是 上的减函数,则 的取值范围是( )A、(0,1) B、 C、 D、11. 已知偶函数 在区间 上单调递增,则满足 的 的取值范围是( )A、 B、 C、 D、12. 已知 是定义域为 的奇函数,满足 .若 ,则 ( )A、 B、 C、 D、二、填空题
-
13. 不论 为何值,函数 的图象一定经过点P,则点P的坐标为.14. 设函数 ,若 ,则实数 .15. 已知 ,则 .16. 设a>0,且a≠1,函数y=a2x+2ax-1在[-1,1]上的最大值是14,则实数a的值为 .
三、解答题
-
17. 化简求值:(1)、 ;(2)、 .18. 已知集合 , .(1)、当 时,求 , ;(2)、若 ,求实数 的取值范围.19. 已知函数 ,且 .(1)、判断函数 的奇偶性;(2)、判断函数 在(1,+∞)上的单调性,并用定义证明你的结论;(3)、若 ,求实数a的取值范围.20. 已知函数 是定义在 上的偶函数,且当 时, .现已画出函数 在 轴左侧的图象,如图所示,请根据图象.
 (1)、写出函数 的增区间;(2)、写出函数 的解析式;(3)、若函数 ,求函数 的最小值.21. 某产品生产厂家生产一种产品,每生产这种产品 (百台),其总成本为 万元 ,其中固定成本为42万元,且每生产1百台的生产成本为15万元 总成本 固定成本 生产成本 销售收入 万元 满足 ,假定该产品产销平衡 即生产的产品都能卖掉 ,根据上述条件,完成下列问题:(1)、写出总利润函数 的解析式 利润 销售收入 总成本 ;(2)、要使工厂有盈利,求产量 的范围;(3)、工厂生产多少台产品时,可使盈利最大?22. 已知指数函数 满足: ,又定义域为 的函数 是奇函数.(1)、确定 的解析式;(2)、求 的值;(3)、若对任意的 ,不等式 恒成立,求实数 的取值范围.
(1)、写出函数 的增区间;(2)、写出函数 的解析式;(3)、若函数 ,求函数 的最小值.21. 某产品生产厂家生产一种产品,每生产这种产品 (百台),其总成本为 万元 ,其中固定成本为42万元,且每生产1百台的生产成本为15万元 总成本 固定成本 生产成本 销售收入 万元 满足 ,假定该产品产销平衡 即生产的产品都能卖掉 ,根据上述条件,完成下列问题:(1)、写出总利润函数 的解析式 利润 销售收入 总成本 ;(2)、要使工厂有盈利,求产量 的范围;(3)、工厂生产多少台产品时,可使盈利最大?22. 已知指数函数 满足: ,又定义域为 的函数 是奇函数.(1)、确定 的解析式;(2)、求 的值;(3)、若对任意的 ,不等式 恒成立,求实数 的取值范围.