2017年山东省日照市莒县中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 如图,数轴上有A,B,C,D四个点,其中表示2的相反数的点是( )
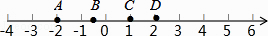 A、点A B、点B C、点C D、点D2. 2017年莒县将以建设莒国古城和开发生态宜居新城为重点,以城带乡、城乡融合,加快推进以人为核心的新型城镇化,在这过程中要完成2.23万套棚户区改造,启动子成范围内15个村和相关单位、居民的搬迁安置,为古城开发打好基础,将2.23万用科学记数法表示为( )A、22.3×103 B、2.23×104 C、0.223×105 D、2.23×1003. 下列运算正确的是( )A、a2•a3=a6 B、5a﹣2a=3a2 C、(a3)4=a12 D、(x+y)2=x2+y24. 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( )
A、点A B、点B C、点C D、点D2. 2017年莒县将以建设莒国古城和开发生态宜居新城为重点,以城带乡、城乡融合,加快推进以人为核心的新型城镇化,在这过程中要完成2.23万套棚户区改造,启动子成范围内15个村和相关单位、居民的搬迁安置,为古城开发打好基础,将2.23万用科学记数法表示为( )A、22.3×103 B、2.23×104 C、0.223×105 D、2.23×1003. 下列运算正确的是( )A、a2•a3=a6 B、5a﹣2a=3a2 C、(a3)4=a12 D、(x+y)2=x2+y24. 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上,则∠1的度数为( ) A、75° B、65° C、45° D、30°5. 如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( )
A、75° B、65° C、45° D、30°5. 如图所示的几何体是由若干大小相同的小立方块搭成,则这个几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( )A、1℃~3℃ B、3℃~5℃ C、5℃~8℃ D、1℃~8℃7. 今年,我市全面启动“精准扶贫”工作,某校为了了解九年级贫困生人数,对该校九年级6个班进行摸排,得到各班贫困生人数分别为12,12,14,10,18,16,这组数据的众数和中位数分别是( )A、12和10 B、12和13 C、12和12 D、12和148. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形9. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠110. 取一张矩形的纸片进行折叠,具体操作过程如下:
6. 甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是( )A、1℃~3℃ B、3℃~5℃ C、5℃~8℃ D、1℃~8℃7. 今年,我市全面启动“精准扶贫”工作,某校为了了解九年级贫困生人数,对该校九年级6个班进行摸排,得到各班贫困生人数分别为12,12,14,10,18,16,这组数据的众数和中位数分别是( )A、12和10 B、12和13 C、12和12 D、12和148. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形9. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠110. 取一张矩形的纸片进行折叠,具体操作过程如下:第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB′E,如图(2);
第三步:沿EB′线折叠得折痕EF,如图(3).
若AB= ,则EF的值是( )
 A、1 B、2 C、3 D、411. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( )
A、1 B、2 C、3 D、411. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个12. 如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
A、1个 B、2个 C、3个 D、4个12. 如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )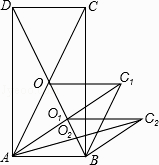 A、cm2 B、cm2 C、cm2 D、cm2
A、cm2 B、cm2 C、cm2 D、cm2二、填空题:
-
13. 分解因式:x3﹣4x= .14. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD= ,AB=5,那么CD的长是 .
 15. 设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 ,以BC为直径作半圆 ,则商标图案(阴影)面积等于 cm2 .
15. 设计一个商标图形(如图8所示),在△ABC中,AB=AC=2cm,∠B=30°,以A为圆心,AB为半径作 ,以BC为直径作半圆 ,则商标图案(阴影)面积等于 cm2 . 16. 如图,点A,B在反比例函数y= (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .
16. 如图,点A,B在反比例函数y= (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是 .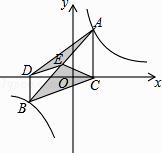
三、解答题:
-
17. 计算题(1)、计算:4sin60°+|3﹣ |﹣( )﹣1+(π﹣2017)0 .(2)、先化简,再求值:( ﹣1)÷ ,其中x的值从不等式组 的整数解中任选一个.18. 为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
 (1)、求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;(2)、学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.19. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?20. 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
(1)、求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;(2)、学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.19. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?20. 如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE. (1)、求证:AB⊥AE;(2)、若BC2=AD•AB,求证:四边形ADCE为正方形.21. 阅读下列材料:
(1)、求证:AB⊥AE;(2)、若BC2=AD•AB,求证:四边形ADCE为正方形.21. 阅读下列材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
 (1)、填空:
(1)、填空:①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, 为半径的圆的方程为 .
(2)、根据以上材料解决下列问题:如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= .

①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
22. 如图,抛物线y=ax2+bx+c经过A(﹣3,0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO. (1)、求抛物线的解析式;(2)、线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)、抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
(1)、求抛物线的解析式;(2)、线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;(3)、抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.