2017年山东省临沂市兰山区中考数学模拟试卷(5月份)
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣ 的倒数是( )A、﹣3 B、3 C、﹣ D、2. 函数y= 中自变量x的取值范围是( )A、x>2 B、x≥2 C、x≤2 D、x≠23. 光速约为300000千米/秒,用科学记数法表示为( )A、3×104千米/秒 B、3×105千米/秒 C、3×106千米/秒 D、30×104千米/秒4. 下列各式计算正确的是( )A、x2•x3=x6 B、2x+3x=5x2 C、x6÷x2=x3 D、(x2)3=x65. 一元二次方程x2+px﹣2=0的一个根为2,则p的值为( )A、1 B、2 C、﹣1 D、﹣26. 我市5月的某一周每天的最高气温(单位:℃)统计如下:19,20,24,22,24,26,27,则这组数据的中位数与众数分别是( )A、23,24 B、24,22 C、24,24 D、22,247. 不等式组 的解集是( )A、﹣2≤x<1 B、﹣2<x≤1 C、﹣1<x≤2 D、﹣1≤x<28. 如图,⊙O是△ABC的外接圆,连接OA、OB,∠OBA=50°,则∠C的度数为( )
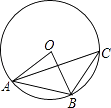 A、30° B、40° C、50° D、80°9. 下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )A、
A、30° B、40° C、50° D、80°9. 下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )A、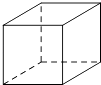 正方体
B、
正方体
B、 圆柱
C、
圆柱
C、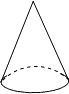 圆椎
D、
圆椎
D、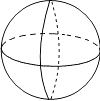 球
10. 在等边三角形、平行四边形、矩形、菱形和圆中,既是轴对称图形又是中心对称图形的有( )A、1种 B、2种 C、3种 D、4种11. 如图,在▱ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )
球
10. 在等边三角形、平行四边形、矩形、菱形和圆中,既是轴对称图形又是中心对称图形的有( )A、1种 B、2种 C、3种 D、4种11. 如图,在▱ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F,则下列结论不一定成立的是( )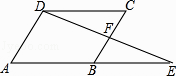 A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF12. 如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
A、∠E=∠CDF B、EF=DF C、AD=2BF D、BE=2CF12. 如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )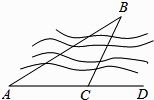 A、100米 B、50 米 C、 米 D、50米13. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A、100米 B、50 米 C、 米 D、50米13. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )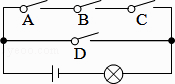 A、 B、 C、 D、14. 如图所示,反比例函数y= 与直线y=﹣x+2只有一个公共点P,则称P为切点.若反比例函数y= 与直线y=kx+6只有一个公共点M,则当k<0时切点M的坐标是( )
A、 B、 C、 D、14. 如图所示,反比例函数y= 与直线y=﹣x+2只有一个公共点P,则称P为切点.若反比例函数y= 与直线y=kx+6只有一个公共点M,则当k<0时切点M的坐标是( )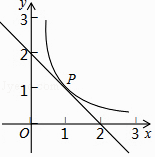 A、(﹣1,3) B、(3,﹣1) C、(1,3) D、(﹣3,1)
A、(﹣1,3) B、(3,﹣1) C、(1,3) D、(﹣3,1)二、填空题
-
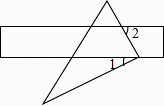
15. 分解因式:2x2﹣8= .16. 将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是 .
 17. 化简: = .18. 小明用图中所示的扇形纸片作一个圆锥侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个圆锥的高是 .
17. 化简: = .18. 小明用图中所示的扇形纸片作一个圆锥侧面,已知扇形的半径为5cm,弧长是6πcm,那么这个圆锥的高是 . 19. 为了求1+2+22+2,3+…2100的值,可令S=1+2+22+23…+2100 , 则2S=2+22+23+…+2101 , 因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+3+32+33+…+32016的值是 .
19. 为了求1+2+22+2,3+…2100的值,可令S=1+2+22+23…+2100 , 则2S=2+22+23+…+2101 , 因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+3+32+33+…+32016的值是 .三、解答题
-
20. 计算:( )﹣2﹣( ﹣ )0+2sin30°+|﹣3|.21. 某校组织了一次初三科技小制作比赛,有A、B、C、D四个班共提供了100件参赛作品.C班提供的参赛作品的获奖率为50%,其他几个班的参赛作品情况及获奖情况绘制在下列图①和图②两幅尚不完整的统计图中.
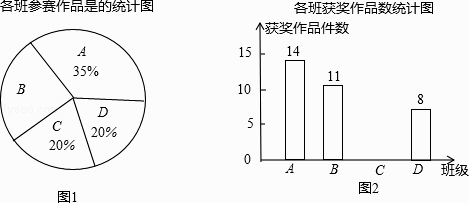 (1)、B班参赛作品有多少件?(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个班的获奖率高?(4)、将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.22. 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究:
(1)、B班参赛作品有多少件?(2)、请你将图②的统计图补充完整;(3)、通过计算说明,哪个班的获奖率高?(4)、将写有A、B、C、D四个字母的完全相同的卡片放入箱中,从中一次随机抽出两张卡片,求抽到A、B两班的概率.22. 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,请探究: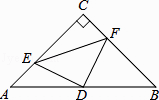 (1)、求证:△DFE是等腰直角三角形;(2)、四边形CEDF的面积是否发生变化?若不变化,请求出面积.23. 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)、求证:△DFE是等腰直角三角形;(2)、四边形CEDF的面积是否发生变化?若不变化,请求出面积.23. 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E. (1)、求证:直线CD为⊙O的切线;(2)、当AB=2BE,且CE= 时,求AD的长.24. 张老师计划组织朋友暑假去旅游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团旅游的游客,甲旅行社表示,每人按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费,假设组团参加甲、乙两家旅行社的人数均为x人.(1)、请分别写出甲、乙两家旅行社收取组团旅游的总费用y(元)与x(人)之间的函数关系式;(2)、若你是张老师,在甲、乙两家旅行社中,你怎样选择?说明理由.25. 已知:如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.
(1)、求证:直线CD为⊙O的切线;(2)、当AB=2BE,且CE= 时,求AD的长.24. 张老师计划组织朋友暑假去旅游,经了解,现有甲、乙两家旅行社比较合适,报价均为每人640元,且提供的服务完全相同,针对组团旅游的游客,甲旅行社表示,每人按八五折收费;乙旅行社表示,若人数不超过20人,每人都按九折收费,超过20人,则超出部分每人按七五折收费,假设组团参加甲、乙两家旅行社的人数均为x人.(1)、请分别写出甲、乙两家旅行社收取组团旅游的总费用y(元)与x(人)之间的函数关系式;(2)、若你是张老师,在甲、乙两家旅行社中,你怎样选择?说明理由.25. 已知:如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH. (1)、求证:∠APB=∠BPH;(2)、当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论.26. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)、求证:∠APB=∠BPH;(2)、当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论.26. 如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)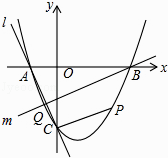 (1)、求抛物线的解析式;(2)、点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.(3)、直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.(3)、直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.