2017年山东省临沂市平邑县中考数学一模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 计算1﹣(﹣2)的正确结果是( )A、﹣2 B、﹣1 C、1 D、32. 钓鱼岛是中国的固有领土,面积约4400000平方米,数据4400000用科学记数法表示应为( )A、44×105 B、0.44×107 C、4.4×106 D、4.4×1053. 已知点M(1﹣2m,m﹣1)关于x轴的对称点在第一象限,则m的取值范围在数轴上表示正确的是( )A、
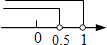 B、
B、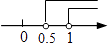 C、
C、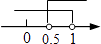 D、
D、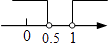 4. 下列运算正确的是( )A、(a2)3=a5 B、a3•a=a4 C、(3ab)2=6a2b2 D、a6÷a3=a25. 下列说法中,正确的是( )A、“打开电视,正在播放新闻联播节目”是必然事件 B、某种彩票中奖概率为10%是指买10张一定有一张中奖 C、了解某种节能灯的使用寿命应采用全面检查 D、一组数据3,5,4,6,7的中位数是5,方差是26. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
4. 下列运算正确的是( )A、(a2)3=a5 B、a3•a=a4 C、(3ab)2=6a2b2 D、a6÷a3=a25. 下列说法中,正确的是( )A、“打开电视,正在播放新闻联播节目”是必然事件 B、某种彩票中奖概率为10%是指买10张一定有一张中奖 C、了解某种节能灯的使用寿命应采用全面检查 D、一组数据3,5,4,6,7的中位数是5,方差是26. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )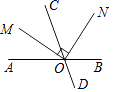 A、65° B、55° C、45° D、35°7. 如图是某几何体的三视图,这个几何体的侧面积是( )
A、65° B、55° C、45° D、35°7. 如图是某几何体的三视图,这个几何体的侧面积是( )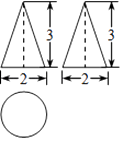 A、6π B、2 π C、 π D、3π8. 分式方程 的解是( )A、x=1 B、x=﹣1 C、x=2 D、x=﹣29. 已知a,b满足方程组 ,则a﹣b的值为( )A、﹣1 B、m﹣1 C、0 D、110. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )
A、6π B、2 π C、 π D、3π8. 分式方程 的解是( )A、x=1 B、x=﹣1 C、x=2 D、x=﹣29. 已知a,b满足方程组 ,则a﹣b的值为( )A、﹣1 B、m﹣1 C、0 D、110. 如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数等于( )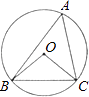 A、60° B、50° C、40° D、30°11. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分图形的面积为( )
A、60° B、50° C、40° D、30°11. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分图形的面积为( )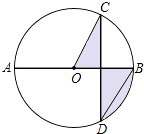 A、4π B、2π C、π D、12.
A、4π B、2π C、π D、12.下列图形中阴影部分的面积相等的是( )
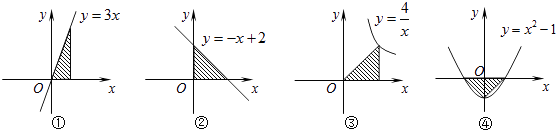 A、②③ B、③④ C、①② D、①④13. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:
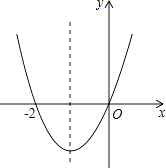
A、②③ B、③④ C、①② D、①④13. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列说法:①c=0;②该抛物线的对称轴是直线x=﹣1;③当x=1时,y=2a;④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
 A、1 B、2 C、3 D、414.
A、1 B、2 C、3 D、414.如图,直线l:y= x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1 , 过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
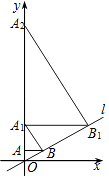 A、(0,42015) B、(0,42014) C、(0,32015) D、(0,32014)
A、(0,42015) B、(0,42014) C、(0,32015) D、(0,32014)二、填空题
-
15. 分解因式:ax2﹣4ay2= .16. 如图,AB和⊙O切于点B,AB=4,OB=2,则tanA= .
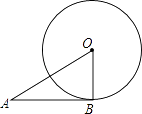 17. 如图,矩形纸片ABCD中,AD=1,将纸片折叠,使顶点A与CD边上的点E重合,折痕FG分别与AD、AB交于点F、G,若DE= ,则EF的长为 .
17. 如图,矩形纸片ABCD中,AD=1,将纸片折叠,使顶点A与CD边上的点E重合,折痕FG分别与AD、AB交于点F、G,若DE= ,则EF的长为 .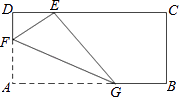 18. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为 .
18. 如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= 的图象上.若点B在反比例函数y= 的图象上,则k的值为 .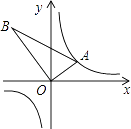 19. 如果一个数的平方等于﹣1,记作i2=﹣1,这个数叫做虚数单位.形如a+bi(a,b为有理数)的数叫复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
19. 如果一个数的平方等于﹣1,记作i2=﹣1,这个数叫做虚数单位.形如a+bi(a,b为有理数)的数叫复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.如:(2+i)+(3﹣5i)=(2+3)+(1﹣5)i=5﹣4i,
(5+i)×(3﹣4i)=5×3+5×(﹣4i)+i×3+i×(﹣4i)=15﹣20i+3i﹣4×i2=15﹣17i﹣4×(﹣1)=19﹣17i.
请根据以上内容的理解,利用以前学习的有关知识将(1+i)(1﹣i)化简结果为为 .
三、解答题
-
20. 计算:( +1)0﹣|sin60°﹣1|﹣ +(﹣1)321.
某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.
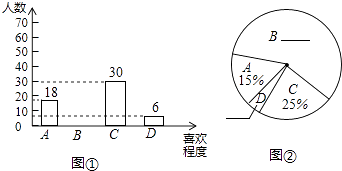
请你根据以上提供的信息,解答下列问题:
(1)、补全上面的条形统计图和扇形统计图;(2)、所抽取学生对数学学习喜欢程度的众数是;(3)、若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?22.某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)
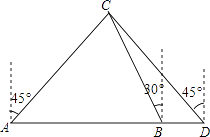 23. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
23. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.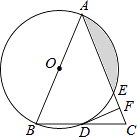 (1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.24. 某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
(1)、求证:DF⊥AC;(2)、若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.24. 某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:类型 价格
进价(元/盏)
售价(元/盏)
A型
30
45
B型
50
70
(1)、若商场预计进货款为3500元,则这两种台灯各购进多少盏?(2)、若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?25. 如图①,四边形ABCD、CEFG均为正方形.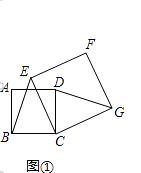 (1)、求证:BE=DG.(2)、如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明.
(1)、求证:BE=DG.(2)、如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.是否仍存在结论BE=DG,若不存在,请说明理由;若存在,给出证明.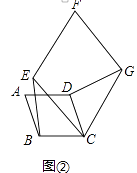 (3)、如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
(3)、如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .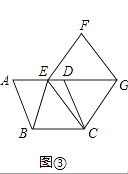 26.
26.如图,二次函数y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
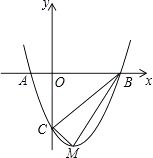 (1)、求该抛物线的解析式;(2)、判断△BCM的形状,并说明理由.(3)、探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.
(1)、求该抛物线的解析式;(2)、判断△BCM的形状,并说明理由.(3)、探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形与△BCM相似?若存在,请求出点P的坐标,若不存在,请说明理由.