2017年山东省济南市槐荫区中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣2是2的( )A、绝对值 B、相反数 C、倒数 D、算术平方根2. 下列立体图形中,俯视图是正方形的是( )A、
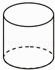 B、
B、 C、
C、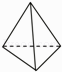 D、
D、 3. 下列计算正确的是( )A、(a5)2=a10 B、x16÷x4=x4 C、2a2+3a2=6a4 D、b3•b3=2b34. 下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是( )A、
3. 下列计算正确的是( )A、(a5)2=a10 B、x16÷x4=x4 C、2a2+3a2=6a4 D、b3•b3=2b34. 下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、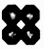 C、
C、 D、
D、 5. 已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )A、3 B、4 C、5 D、66. 不等式1+x<0的解集在数轴上表示正确的是( )A、
5. 已知一组数据3,a,4,5的众数为4,则这组数据的平均数为( )A、3 B、4 C、5 D、66. 不等式1+x<0的解集在数轴上表示正确的是( )A、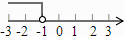 B、
B、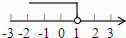 C、
C、 D、
D、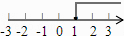 7. “a是实数,|a|<0”这一事件是( )A、必然事件 B、不确定事件 C、不可能事件 D、随机事件8. 下列说法中,正确的是( )A、同位角相等 B、矩形的对角线一定互相垂直 C、对角线相等的四边形是矩形 D、四条边相等的四边形是菱形9. 若宇宙中一块陨石落在地球上,它落在陆地上的概率是0.3,那么用扇形统计图反映地球上陆地面积与海洋面积所占的比例时,陆地面积所对应的圆心角是( )A、54° B、72° C、108° D、114°10. 计算 的结果是( )A、0 B、1 C、﹣1 D、x11. 将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )A、y=3(x+2)2+3 B、y=3(x﹣2)2+3 C、y=3(x+2)2﹣3 D、y=3(x﹣2)2﹣312. 如图,在Rt△ABO中,斜边AB=1.若OC//BA,∠AOC=36°,则( )
7. “a是实数,|a|<0”这一事件是( )A、必然事件 B、不确定事件 C、不可能事件 D、随机事件8. 下列说法中,正确的是( )A、同位角相等 B、矩形的对角线一定互相垂直 C、对角线相等的四边形是矩形 D、四条边相等的四边形是菱形9. 若宇宙中一块陨石落在地球上,它落在陆地上的概率是0.3,那么用扇形统计图反映地球上陆地面积与海洋面积所占的比例时,陆地面积所对应的圆心角是( )A、54° B、72° C、108° D、114°10. 计算 的结果是( )A、0 B、1 C、﹣1 D、x11. 将抛物线y=3x2向上平移3个单位,再向左平移2个单位,那么得到的抛物线的解析式为( )A、y=3(x+2)2+3 B、y=3(x﹣2)2+3 C、y=3(x+2)2﹣3 D、y=3(x﹣2)2﹣312. 如图,在Rt△ABO中,斜边AB=1.若OC//BA,∠AOC=36°,则( ) A、点B到AO的距离为sin54° B、点B到AO的距离为tan36° C、点A到OC的距离为sin36°sin54° D、点A到OC的距离为cos36°sin54°13. 如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A、点B到AO的距离为sin54° B、点B到AO的距离为tan36° C、点A到OC的距离为sin36°sin54° D、点A到OC的距离为cos36°sin54°13. 如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( ) A、 B、2 C、 D、14. 如图,抛物线y= x2﹣ x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( )
A、 B、2 C、 D、14. 如图,抛物线y= x2﹣ x﹣2与x轴交于A、B两点,点P(m,n)(n<0)为抛物线上一个动点,当∠APB为钝角时,则m的取值范围( ) A、﹣1<m<0 B、﹣1<m<0或3<m<4 C、0<m<3或m>4 D、m<﹣1或0<m<315. 阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
A、﹣1<m<0 B、﹣1<m<0或3<m<4 C、0<m<3或m>4 D、m<﹣1或0<m<315. 阅读理解:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
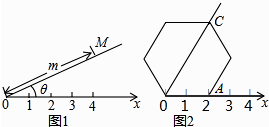 A、(60°,4) B、(45°,4) C、(60°,2 ) D、(50°,2 )
A、(60°,4) B、(45°,4) C、(60°,2 ) D、(50°,2 )二、填空题
-
16. 化简:2(a+1)﹣a= .17. 分解因式:mn2﹣4m= .18. 据济南市政府网站发布的消息知,济南已拆除违建面积991000平方米,991000用科学记数法表示为 .19. 如图,圆内接四边形ABDC,延长BA和DC相交于圆外一点P,∠P=30°,∠D=70°,则∠ACP= .
 20. 已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x﹣2上一个动点,当|PB﹣PA|值最大时,点P的坐标为 .
20. 已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x﹣2上一个动点,当|PB﹣PA|值最大时,点P的坐标为 . 21. 如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= (k≠0)上的点D1处,则a= .
21. 如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y= (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y= (k≠0)上的点D1处,则a= .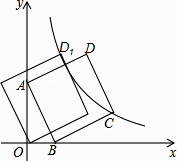
三、解答题
-
22. 计算:( ﹣3)0﹣ +|﹣2|23. 求不等式组 的解集并把解集表示在数轴上.24. 图,点E、F在AC上,AB//CD,AB=CD,AE=CF,求证:△ABF≌△CDE.
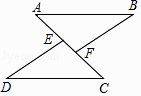 25. 如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,若∠AEB=∠CFD.
25. 如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF,若∠AEB=∠CFD.求证:四边形AECF是平行四边形.
 26. 某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元
26. 某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元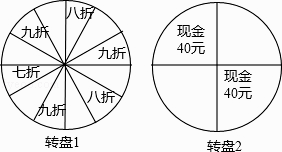 (1)、若他选择转动转盘1,则他能得到优惠的概率为多少?(2)、选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.27. 小明到离家2400米的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有40分钟,于是他立即步行(匀速)回家取票,在家取票用时2分钟,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20分钟,骑自行车的速度是步行速度的3倍.(1)、小明步行的速度(单位:米/分钟)是多少?(2)、小明能否在球赛开始前赶到体育馆?28. 如图,直线l1:y=kx+b平行于直线y=x﹣1,且与直线l2: 相交于点P(﹣1,0).
(1)、若他选择转动转盘1,则他能得到优惠的概率为多少?(2)、选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.27. 小明到离家2400米的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有40分钟,于是他立即步行(匀速)回家取票,在家取票用时2分钟,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20分钟,骑自行车的速度是步行速度的3倍.(1)、小明步行的速度(单位:米/分钟)是多少?(2)、小明能否在球赛开始前赶到体育馆?28. 如图,直线l1:y=kx+b平行于直线y=x﹣1,且与直线l2: 相交于点P(﹣1,0). (1)、求直线l1、l2的解析式;(2)、直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…
(1)、求直线l1、l2的解析式;(2)、直线l1与y轴交于点A.一动点C从点A出发,先沿平行于x轴的方向运动,到达直线l2上的点B1处后,改为垂直于x轴的方向运动,到达直线l1上的点A1处后,再沿平行于x轴的方向运动,到达直线l2上的点B2处后,又改为垂直于x轴的方向运动,到达直线l1上的点A2处后,仍沿平行于x轴的方向运动,…照此规律运动,动点C依次经过点B1 , A1 , B2 , A2 , B3 , A3 , …,Bn , An , …
①求点B1 , B2 , A1 , A2的坐标;
②请你通过归纳得出点An、Bn的坐标;并求当动点C到达An处时,运动的总路径的长?
29. 如图,直角梯形ABCD中,AB//DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C﹣D﹣A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l//AD,与线段CD的交点为E,与折线A﹣C﹣B的交点为Q.点M运动的时间为t(秒). (1)、当t=0.5时,求线段QM的长;(2)、当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;(3)、当t>2时,连接PQ交线段AC于点R.请探究 是否为定值,若是,试求这个定值;若不是,请说明理由.30. 我们常见的炒菜锅和锅盖都是抛物面,经过锅心和盖心的纵断面是由两段抛物线组合而成的封闭图形,不妨简称为“锅线”.锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图1所示,如果把锅纵断面的抛物线记为C1 , 把锅盖纵断面的抛物线记为C2 .
(1)、当t=0.5时,求线段QM的长;(2)、当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;(3)、当t>2时,连接PQ交线段AC于点R.请探究 是否为定值,若是,试求这个定值;若不是,请说明理由.30. 我们常见的炒菜锅和锅盖都是抛物面,经过锅心和盖心的纵断面是由两段抛物线组合而成的封闭图形,不妨简称为“锅线”.锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图1所示,如果把锅纵断面的抛物线记为C1 , 把锅盖纵断面的抛物线记为C2 . (1)、求C1和C2的解析式;(2)、如图2,过点B作直线BE:y= x﹣1交C1于点E(﹣2,﹣ ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(1)、求C1和C2的解析式;(2)、如图2,过点B作直线BE:y= x﹣1交C1于点E(﹣2,﹣ ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;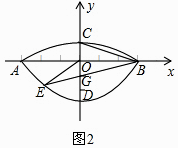 (3)、如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.
(3)、如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.