2017年山东省聊城市冠县中考数学二模试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 下列四个选项中,计算结果最大的是( )A、(﹣6)0 B、|﹣6| C、﹣6 D、2. 把一块直尺与三角板如图放置,若∠1=40°,则∠2的度数为( )
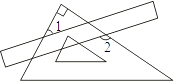 A、130° B、140° C、12° D、125°3. 如图是一个由7个相同正方体组合而成的几何体,它的主视图为( )
A、130° B、140° C、12° D、125°3. 如图是一个由7个相同正方体组合而成的几何体,它的主视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列事件中,属于必然事件的是( )A、投掷一枚均匀的硬币100次,正面朝上的次数为50次 B、任意一个一元二次方程都有实数根 C、三角形的外心在三角形的外部 D、直角三角形的形斜边上的中线等于斜边的一般5. 下列运算正确的是( )A、3 =3 B、(2x2)3=2x5 C、2a•5b=10ab D、 ÷ =26. 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
4. 下列事件中,属于必然事件的是( )A、投掷一枚均匀的硬币100次,正面朝上的次数为50次 B、任意一个一元二次方程都有实数根 C、三角形的外心在三角形的外部 D、直角三角形的形斜边上的中线等于斜边的一般5. 下列运算正确的是( )A、3 =3 B、(2x2)3=2x5 C、2a•5b=10ab D、 ÷ =26. 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )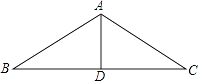 A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米7. 某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:
A、5sin36°米 B、5cos36°米 C、5tan36°米 D、10tan36°米7. 某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如表:成绩(分)
35
39
42
44
45
48
50
人数(人)
2
5
6
6
8
7
6
根据表中的信息判断,下列结论中错误的是( )
A、该班一共有40名同学 B、该班学生这次考试成绩的众数是45分 C、该班学生这次考试成绩的中位数是45分 D、该班学生这次考试成绩的平均数是45分8. 不等式 > ﹣1的正整数解的个数是( )A、1个 B、2个 C、3个 D、4个9. 把多项式x2+ax+b分解因式,得(x+1)(x﹣3)则a,b的值分别是( )A、a=2,b=3 B、a=﹣2,b=﹣3 C、a=﹣2,b=3 D、a=2,b=﹣310. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(﹣2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )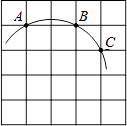 A、(0,0) B、(﹣1,1) C、(﹣1,0) D、(﹣1,﹣1)11.
A、(0,0) B、(﹣1,1) C、(﹣1,0) D、(﹣1,﹣1)11.如图,在矩形中截取两个相同的正方形作为立方体的上下底面,剩余的矩形作为立方体的侧面,刚好能组成立方体.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
 A、
A、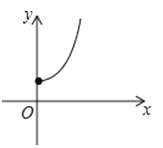 B、
B、 C、
C、 D、
D、 12. 如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y= 的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+ n=0;③S△AOP=S△BOQ;④不等式k1x+b> 的解集在x<﹣2或0<x<1,其中正确的结论是( )
12. 如图,已知直线y=k1x+b与x轴,y轴相交于P,Q两点,则y= 的图象相交于A(﹣2,m),B(1,n)两点,连接OA,OB,给出下列结论:①k1k2<0;②m+ n=0;③S△AOP=S△BOQ;④不等式k1x+b> 的解集在x<﹣2或0<x<1,其中正确的结论是( ) A、②③④ B、①②③④ C、③④ D、②③
A、②③④ B、①②③④ C、③④ D、②③二、填空题
-
13. 函数y= 中自变量x的取值范围是 .14.
如图,直线y= x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
 15. 一个不透明的袋子中装有仅颜色不同的2个红球和2个白球,两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是 .16. 一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为 .
15. 一个不透明的袋子中装有仅颜色不同的2个红球和2个白球,两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是 .16. 一个圆锥形漏斗,某同学用三角波测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为 . 17. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .
17. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 矩形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=秒时,S1=2S2 .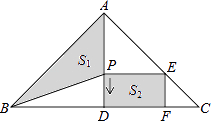
三、解答题
-
18. 化简:(1﹣ )÷ .19. 如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于 AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
 (1)、求证:△AED≌△CFD;(2)、求证:四边形AECF是菱形.20. 为了方便居民低碳出行,2015年12月30日,湘潭市公共自行车租赁系统(一期)试运行以来,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出).
(1)、求证:△AED≌△CFD;(2)、求证:四边形AECF是菱形.20. 为了方便居民低碳出行,2015年12月30日,湘潭市公共自行车租赁系统(一期)试运行以来,越来越多的居民选择公共自行车作为出行的交通工具,市区某中学课外兴趣小组为了了解某小区居民出行方式的变化情况,随机抽取了该小区部分居民进行调查,并绘制了如图的条形统计图和扇形统计图(部分信息未给出).
请根据上面的统计图,解答下列问题:
(1)、被调查的总人数是人;(2)、公共自行车租赁系统运行后,被调查居民选择自行车作为出行方式的百分比提高了多少?(3)、如果该小区共有居民2000人,公共自行车租赁系统运行后估计选择自行车作为出行方式的有多少人?21. 现在正是草莓热销的季节,某水果零售商店分两批次从批发市场共购进草莓40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.(1)、设第一、二次购进草莓的箱数分别为a箱、b箱,求a,b的值;(2)、若商店对这40箱草莓先按每箱60元销售了x箱,其余的按每箱35元全部售完.①求商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入﹣进货总成本)
22.为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60( )海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120( )海里.
 (1)、分别求出A与C及B与C的距离AC、BC(结果保留根号)(2)、已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?
(1)、分别求出A与C及B与C的距离AC、BC(结果保留根号)(2)、已知在灯塔D周围100海里范围内有暗礁群,我在A处海监船沿AC前往C处盘查,图中有无触礁的危险?(参考数据: =1.41, =1.73, =2.45)
23. 在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y= (k>0)图象与AC边交于点E. (1)、请用k表示点E,F的坐标;(2)、若△OEF的面积为9,求反比例函数的解析式.24. 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)、请用k表示点E,F的坐标;(2)、若△OEF的面积为9,求反比例函数的解析式.24. 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F. (1)、求证:DF⊥AC;(2)、若⊙O的半径为5,∠CDF=30°,求 的长(结果保留π).25.
(1)、求证:DF⊥AC;(2)、若⊙O的半径为5,∠CDF=30°,求 的长(结果保留π).25.如图,已知抛物线y=﹣ x2+bx+4与x轴相交于A,B两点,与y轴相交于点C,若已知B点的坐标为B(8,0)
 (1)、求抛物线的解析式及其对称轴.(2)、连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.(3)、M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;(4)、在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及其对称轴.(2)、连接AC、BC,试判断△AOC与△COB是否相似?并说明理由.(3)、M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;(4)、在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.