2017年山东省德州市宁津县中考数学模拟试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. ﹣5的相反数是( )A、﹣5 B、5 C、﹣ D、2. 下列计算正确的是( )A、( )﹣2=9 B、 =﹣2 C、(﹣2)0=﹣1 D、|﹣5﹣3|=23. 2016年3月份我省农产品实现出口额8362万美元,其中8362万用科学记数法表示为( )A、8.362×107 B、83.62×106 C、0.8362×108 D、8.362×1084. 下面几何体中,其主视图与俯视图相同的是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列说法中正确的是( )A、“打开电视,正在播放《新闻联播》”是必然事件 B、“x2<0(x是实数)”是随机事件 C、掷一枚质地均匀的硬币10次,可能有5次正面向上 D、为了了解夏季冷饮市场上冰淇淋的质量情况,宜采用普查方式调查6. 小明在计算三角形面积时需要作出最长边的垂线段,下列作法正确的是( )A、
5. 下列说法中正确的是( )A、“打开电视,正在播放《新闻联播》”是必然事件 B、“x2<0(x是实数)”是随机事件 C、掷一枚质地均匀的硬币10次,可能有5次正面向上 D、为了了解夏季冷饮市场上冰淇淋的质量情况,宜采用普查方式调查6. 小明在计算三角形面积时需要作出最长边的垂线段,下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 不等式组 的解集在数轴上表示为( )A、
7. 不等式组 的解集在数轴上表示为( )A、 B、
B、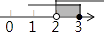 C、
C、 D、
D、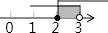 8. 顺次连结矩形四边中点所得的四边形一定是( )A、菱形 B、矩形 C、正方形 D、等腰梯形9. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( )
8. 顺次连结矩形四边中点所得的四边形一定是( )A、菱形 B、矩形 C、正方形 D、等腰梯形9. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( ) A、120° B、135° C、150° D、165°10. 给出下列函数:①y=2x;②y=﹣2x+1;③(x>0);④y=x2(x<1),其中y随x的增大而减小的函数是( )A、①②③④ B、②③④ C、②④ D、②③11. 观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则:81+82+83+84+…+82017 的个位数字是( )A、2 B、4 C、6 D、812. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( )
A、120° B、135° C、150° D、165°10. 给出下列函数:①y=2x;②y=﹣2x+1;③(x>0);④y=x2(x<1),其中y随x的增大而减小的函数是( )A、①②③④ B、②③④ C、②④ D、②③11. 观察下列运算:81=8,82=64,83=512,84=4096,85=32768,86=262144,…,则:81+82+83+84+…+82017 的个位数字是( )A、2 B、4 C、6 D、812. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc=0,②a+b+c>0,③a>b,④4ac﹣b2<0;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题:
-
13. 化简: = .14. 式子 在实数范围内有意义,则 x 的取值范围是 .15. 若方程 x2﹣4x﹣1=0 的两根分别是x1 , x2 , 则x12+x22= .16. 如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为 .
 17. 如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:
17. 如图,△ABC是等腰三角形,∠C=90°,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE,DF,EF.在此运动变化过程中,有下列结论:①DE=DF;
②∠EDF=90°;
③四边形CEDF不可能为正方形;
④四边形CEDF的面积保持不变.
一定成立的结论有(把你认为正确的序号都填上)

三、解答题:
-
18. 先化简,再求代数式( ﹣ )÷ 的值,其中a=2sin60°+tan45°.19. 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表
候选教师
丁老师
俞老师
李老师
陈老师
得票数
200
300
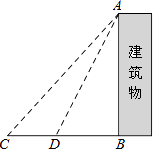
(1)、若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)(2)、丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?(3)、在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?20. 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)(参考数据:sin48°≈ ,tan48°≈ ,sin64°≈ ,tan64°≈2)
 21. 如图,平行于y轴的直尺(一部分)与双曲线y= (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.
21. 如图,平行于y轴的直尺(一部分)与双曲线y= (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm. (1)、求k的值;(2)、求经过A、C两点的直线的解析式;(3)、连接OA、OC,求△OAC的面积.22. 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)、求k的值;(2)、求经过A、C两点的直线的解析式;(3)、连接OA、OC,求△OAC的面积.22. 如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF. (1)、求证:CB是⊙O的切线;(2)、若∠ECB=60°,AB=6,求图中阴影部分的面积.23. 如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)、求证:CB是⊙O的切线;(2)、若∠ECB=60°,AB=6,求图中阴影部分的面积.23. 如图1,我们把对角线互相垂直的四边形叫做垂美四边形. (1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由. (2)、性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
(2)、性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)、问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长. 24. 如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
24. 如图,在平面直角坐标系中,直线y=﹣3x﹣3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧). (1)、求抛物线的解析式及点B坐标;(2)、若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;(3)、试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
(1)、求抛物线的解析式及点B坐标;(2)、若点M是线段BC上一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;(3)、试探究当ME取最大值时,在x轴下方抛物线上是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.