2017年内蒙古鄂尔多斯市鄂托克旗中考数学模拟试卷
试卷更新日期:2017-07-20 类型:中考模拟
一、选择题
-
1. 如图,数轴上的点P表示的数可能是( )
 A、 B、﹣ C、﹣3.8 D、﹣2. 下列计算中,正确的是( )A、x3•x2=x6 B、x3﹣x2=x C、(﹣x)2•(﹣x)=﹣x3 D、x6÷x2=x33. 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( )
A、 B、﹣ C、﹣3.8 D、﹣2. 下列计算中,正确的是( )A、x3•x2=x6 B、x3﹣x2=x C、(﹣x)2•(﹣x)=﹣x3 D、x6÷x2=x33. 如图,四边形纸片ABCD中,∠A=70°,∠B=80°,将纸片折叠,使C,D落在AB边上的C′,D′处,折痕为MN,则∠AMD′+∠BNC′=( ) A、50° B、60° C、70° D、80°4. PM2.5是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )A、2.5×10﹣7 B、2.5×10﹣6 C、25×10﹣7 D、0.25×10﹣55. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
A、50° B、60° C、70° D、80°4. PM2.5是指大气中直径≤0.0000025米的颗粒物,将0.0000025用科学记数法表示为( )A、2.5×10﹣7 B、2.5×10﹣6 C、25×10﹣7 D、0.25×10﹣55. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、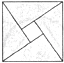 B、
B、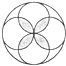 C、
C、 D、
D、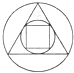 6. 互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )A、120元 B、100元 C、80元 D、60元7. 下列说法正确的是( )A、一个游戏的中奖概率是 ,则做10次这样的游戏一定会中奖 B、一组数据6,8,7,8,8,9,10的众数和中位数都是8 C、为了解全国中学生的心理健康情况,应该采用普查的方式 D、若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定8. 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
6. 互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )A、120元 B、100元 C、80元 D、60元7. 下列说法正确的是( )A、一个游戏的中奖概率是 ,则做10次这样的游戏一定会中奖 B、一组数据6,8,7,8,8,9,10的众数和中位数都是8 C、为了解全国中学生的心理健康情况,应该采用普查的方式 D、若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定8. 如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )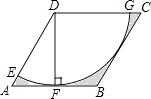 A、18 ﹣9π B、18﹣3π C、9 ﹣ D、18 ﹣3π9. 定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min={1,﹣2}=﹣2,min{﹣1,2}=﹣1.则min{x2﹣1,﹣2}的值是( )A、x2﹣1 B、2 C、﹣1 D、﹣210. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A、18 ﹣9π B、18﹣3π C、9 ﹣ D、18 ﹣3π9. 定义符号min{a,b}的含义为:当a≥b时,min{a,b}=b;当a<b时,min{a,b}=a.如:min={1,﹣2}=﹣2,min{﹣1,2}=﹣1.则min{x2﹣1,﹣2}的值是( )A、x2﹣1 B、2 C、﹣1 D、﹣210. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )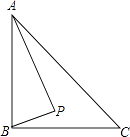 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题.
-
11. 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个二次三项式,形式如下:
 ﹣3x=x2﹣5x+1,若x= ,则所捂二次三项式的值为 . 12. 函数y= 的自变量x的取值范围是 .13. 不等式组 的解集是 .14. 如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2=°.
﹣3x=x2﹣5x+1,若x= ,则所捂二次三项式的值为 . 12. 函数y= 的自变量x的取值范围是 .13. 不等式组 的解集是 .14. 如图,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2=°. 15. “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是 .
15. “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).小亮随机地向大正方形内部区域投飞镖.若直角三角形两条直角边的长分别是2和1,则飞镖投到小正方形(阴影)区域的概率是 . 16. 观察下列等式
16. 观察下列等式12=1= ×1×2×(2+1)
12+22= ×2×3×(4+1)
12+22+32= ×3×4×(6+1)
12+22+32+42= ×4×5×(8+1)…
可以推测12+22+32+…+n2= .
三、解答题
-
17. 综合题。(1)、计算:﹣22+| ﹣4|+( )﹣1+2tan60°.(2)、先化简,再求值:( ﹣ )÷ ,其中x是不等式3x+7>1的负整数解.18. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t)
频数
百分比
2≤x<3
2
4%
3≤x<4
12
24%
4≤x<5
5≤x<6
10
20%
6≤x<7
12%
7≤x<8
3
6%
8≤x<9
2
4%
 (1)、请根据题中已有的信息补全频数分布表和频数分布直方图;(2)、如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?(3)、从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.19. 如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ).
(1)、请根据题中已有的信息补全频数分布表和频数分布直方图;(2)、如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?(3)、从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.19. 如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ).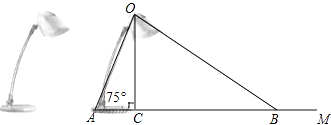 20. 如图,一次函数y=kx+b(k<0)与反比例函数y= 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
20. 如图,一次函数y=kx+b(k<0)与反比例函数y= 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) (1)、求反比例函数的解析式;(2)、连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.21. 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
(1)、求反比例函数的解析式;(2)、连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.21. 为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元. (1)、求A,B两种品牌的足球的单价.(2)、求该校购买20个A品牌的足球和2个B品牌的足球的总费用.22. 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
(1)、求A,B两种品牌的足球的单价.(2)、求该校购买20个A品牌的足球和2个B品牌的足球的总费用.22. 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C. (1)、求证:PB是⊙O的切线;(2)、连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ,求BC的长.23. 已知△ABC是等腰直角三角形,∠BAC=90°,CD= BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.(1)、如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长;
(1)、求证:PB是⊙O的切线;(2)、连接OP,若OP∥BC,且OP=8,⊙O的半径为2 ,求BC的长.23. 已知△ABC是等腰直角三角形,∠BAC=90°,CD= BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.(1)、如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长; (2)、如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证:MN⊥AE;
(2)、如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证:MN⊥AE; (3)、如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索 的值并直接写出结果.
(3)、如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索 的值并直接写出结果. 24. 如图,已知抛物线与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于点C(0,5).
24. 如图,已知抛物线与x轴交于A(﹣1,0)、B(5,0)两点,与y轴交于点C(0,5). (1)、求该抛物线所对应的函数关系式;(2)、D是笫一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD.设点D的横坐标为m,△BCD的面积为S.
(1)、求该抛物线所对应的函数关系式;(2)、D是笫一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD.设点D的横坐标为m,△BCD的面积为S.①求S关于m的函数关系式及自变量m的取值范围;
②当m为何值时,S有最大值,并求这个最大值;
③直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.