2017年内蒙古巴彦淖尔市乌拉特前旗中考数学模拟试卷（4月份）

试卷更新日期：2017-07-20 类型：中考模拟

进入出卷网下载

一、单项选择题

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列各式的变形中，正确的是（）

A、（﹣x﹣y）（﹣x+y）=x²﹣y² B、 $\frac{1}{x}$ ﹣x= $\frac{1 - x}{x}$ C、x²﹣4x+3=（x﹣2）²+1 D、x÷（x²+x）= $\frac{1}{x}$ +1

查看试题解析
3. 已知点M、N、P、Q在数轴上的位置如图，则其中对应的数的绝对值最大的点是（）

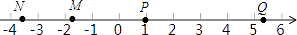A、M B、N C、P D、Q

查看试题解析
4.
下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图，某学校九年级（1）班45名同学每周课外阅读时间的频数直方图（每组含前一个边界值，不含后一个边界值）．由图可知，人数最多的一组是（）

A、2﹣4小时 B、4﹣6小时 C、6﹣8小时 D、8﹣10小时

查看试题解析
6. 如图所示，△ABC中，点D、E分别是AC、BC边上的点，且DE∥AB，CD：CA﹦2：3，△ABC的面积是18，则△DEC的面积是（）

A、8 B、9 C、12 D、15

查看试题解析
7. 如图，已知点A（0，1），B（0，﹣1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于（）

A、90° B、120° C、60° D、30°

查看试题解析
8. 如图A，B，C是⊙O上的三个点，若∠AOC=100°，则∠ABC等于（）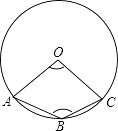

A、50° B、80° C、100° D、130°

查看试题解析
9. 如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（）

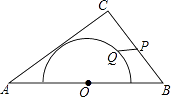A、6 B、2 $\sqrt{13}$ +1 C、9 D、 $\frac{32}{2}$

查看试题解析
10. 如图，已知E、F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M，O为BD的中点，则下列结论：①∠AME=90°；②∠BAF=∠EDB；③∠BMO=90°；④MD=2AM=4EM；⑤AM= $\frac{2}{3}$ MF．其中正确结论的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 一次数学模考后，刘老师统计了20名学生的成绩，记录如下：有6人得了85分，有5人得了80分，有4人得了65分，有5人得了90分．则这组数据的中位数和平均数分别是．

查看试题解析
12. 在函数y= $\frac{1}{\sqrt{x + 1}}$ +（x﹣2）⁰中，自变量x的取值范围是．

查看试题解析
13. 如图，若点A的坐标为 $(1 ， \sqrt{3})$ ，则sin∠1= ．

查看试题解析
14. 如图，正方形ABCD的边长为2，H在CD的延长线上，四边形CEFH也为正方形，则△DBF的面积为．

查看试题解析
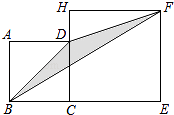15. 如图，四边形ABCD是菱形，∠A=60°，AB=6，扇形BEF的半径为6，圆心角为60°，则图中阴影部分的面积是．

查看试题解析
16.
如图，把同样大小的黑色棋子摆放在正多边形的边上，第一个图形需要3个黑色棋子，第二个图形需要8个黑色棋子，…，按照这样的规律摆下去，第n（n是正整数）个图形需要黑色棋子的个数是（用含n的代数式表示）．

查看试题解析

三、计算题

17. 综合题。

(1)、计算题：|﹣3|+ $\sqrt{3}$ tan30°﹣ $\sqrt[3]{8}$ ﹣（2017﹣π）⁰+（ $\frac{1}{3}$ ）^﹣¹

(2)、计算题：（x﹣2﹣ $\frac{12}{x + 2}$ ）÷ $\frac{4 - x}{x + 2}$

(3)、解不等式组： ${\begin{matrix} x - 3 (x - 2) \leq 4 \\ \frac{x - 1}{2} < \frac{x + 1}{3} \end{matrix}$ ．

查看试题解析
18.
如图，小岛在港口P的北偏西60°方向，距港口56海里的A处，货船从港口P出发，沿北偏东45°方向匀速驶离港口P，4小时后货船在小岛的正东方向．求货船的航行速度．（精确到0.1海里/时，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
19.
某商场服装部为了解服装的销售情况，统计了每位营业员在某月的销售额（单位：万元），并根据统计的这组数据，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题．
（Ⅰ）该商场服装部营业员的人数为 $\underline{}$ ，图①中m的值为 $\underline{}$ .
（Ⅱ）求统计的这组销售额额数据的平均数、众数和中位数．

查看试题解析
20. 在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有1、2、3的蓝色卡片，卡片除颜色和数字外其它完全相同．

(1)、从中任意抽取一张卡片，求该卡片上写有数字1的概率；

(2)、将3张蓝色卡片取出后放入另外一个不透明的盒子内，然后在两个盒子内各任意抽取一张卡片，以红色卡片上的数字作为十位数，蓝色卡片上的数字作为个位数组成一个两位数，求这个两位数不小于22的概率（请利用树状图或列表法说明）

查看试题解析
21. 如图，△ABC中，AB=AC=1，∠BAC=45°，△AEF是由△ABC绕点A按顺时针方向旋转得到的，连接BE、CF相交于点D．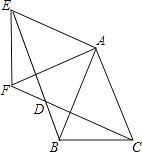

(1)、求证：BE=CF；

(2)、当四边形ACDE为菱形时，求BD的长．

查看试题解析
22. 某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克，如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完．

(1)、该种干果的第一次进价是每千克多少元？

(2)、超市销售这种干果共盈利多少元？

查看试题解析
23. 如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连接AD并延长，交BE于点E．

(1)、求证：AB=BE；

(2)、若PA=2，cosB= $\frac{3}{5}$ ，求⊙O半径的长．

查看试题解析
24.
如图，已知抛物线经过A（﹣2，0）B（﹣3，3）及原点O，顶点为C．

(1)、求抛物线的解析式；

(2)、若点E在抛物线的对称轴上，且A、O、D、E为顶点是四边形是平行四边形，求点D的坐标．

(3)、P是抛物线上的第一象限内的动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形△BOC相似？

查看试题解析